Robot de equilibrio automático con algoritmo PID (STM MC): 9 pasos

2024 Autor: John Day | [email protected]. Última modificación: 2024-01-30 08:43

Recientemente se ha trabajado mucho en el autoequilibrio de objetos. El concepto de autoequilibrio comenzó con el equilibrio del péndulo invertido. Este concepto se extendió también al diseño de aeronaves. En este proyecto, hemos diseñado un pequeño modelo de robot autoequilibrante utilizando el algoritmo PID (Proporcional, Integral, Derivado). Desde entonces, este método es la nueva cara de los sistemas de control de procesos industriales. Este informe revisa los métodos involucrados en el autoequilibrio de objetos. Este proyecto se llevó a cabo como un proyecto semestral para comprender la correlación de PID en la eficiencia de varios procesos industriales. Aquí nos enfocamos solo en brindar una breve revisión de la efectividad y aplicación del control PID. Este documento ha sido desarrollado proporcionando una breve introducción a los sistemas de control y terminologías relacionadas, además de las motivaciones del proyecto. Se han realizado experimentos y observaciones, describiendo méritos y deméritos con finalización en las futuras mejoras. Se desarrolló un modelo de robot autoequilibrado para comprender la efectividad de PID en el mundo del sistema de control. Pasando por algunas pruebas y experimentos rigurosos, se descubrieron los méritos y desventajas del sistema de control PID. Se descubrió que, a pesar de las muchas ventajas del control PID sobre los métodos anteriores, este sistema aún requiere muchas mejoras. Se espera que el lector comprenda bien la importancia del autoequilibrio, la efectividad y las deficiencias del control PID.

Paso 1: Introducción

Con el advenimiento de las computadoras y la industrialización de los procesos, a lo largo de la historia del hombre, siempre ha habido investigaciones para desarrollar formas de refinar los procesos y, lo que es más importante, controlarlos utilizando máquinas de forma autónoma. El propósito es reducir la participación del hombre en estos procesos, reduciendo así el error en estos procesos. Por lo tanto, se desarrolló el campo de la”Ingeniería de sistemas de control”. La ingeniería del sistema de control puede definirse como el uso de varios métodos para controlar el funcionamiento de un proceso o el mantenimiento de un entorno constante y preferido, ya sea manual o automático.

Un ejemplo simple podría ser el control de la temperatura en una habitación. Control manual significa la presencia de una persona en un sitio que verifica las condiciones presentes (sensor), lo compara con el valor deseado (procesamiento) y toma la acción apropiada para obtener el valor deseado (actuador). El problema con este método es que no es muy confiable ya que una persona es propensa a cometer errores o negligencia en su trabajo. Además, otro problema es que la velocidad del proceso iniciado por el actuador no siempre es uniforme, lo que significa que a veces puede ocurrir más rápido de lo requerido o, a veces, puede ser lento. La solución a este problema fue utilizar un microcontrolador para controlar el sistema. El microcontrolador es

programado para controlar el proceso, de acuerdo con especi fi caciones dadas, conectado en un circuito (que se discutirá más adelante), alimentado el valor o las condiciones deseadas y, por lo tanto, controla el proceso para mantener el valor deseado. La ventaja de este proceso es que no se requiere intervención humana en este proceso. Además, la velocidad del proceso es uniforme.

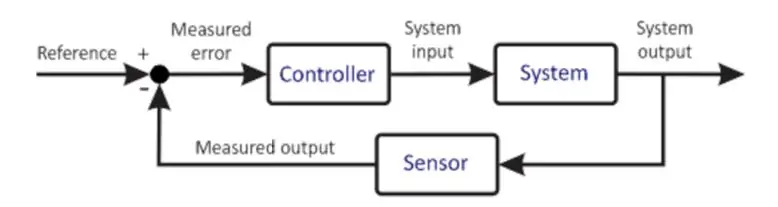
Sistema de control básico

El diagrama anterior muestra una versión muy simplificada de un sistema de control. El microcontrolador está en el corazón de cualquier sistema de control. Es un componente muy importante, por lo tanto, su elección de selección debe realizarse cuidadosamente en función de los requisitos del Sistema. El microcontrolador recibe una entrada del usuario. Esta entrada de fi ne la condición deseada del sistema. El microcontrolador también recibe una entrada de retroalimentación del sensor. Este sensor está conectado a la salida del sistema, cuya información se retroalimenta a la entrada. El microprocesador, basado en su programación, realiza varios cálculos y da una salida al actuador. El actuador, basado en la salida, controla la planta para tratar de mantener esas condiciones. Un ejemplo podría ser un controlador de motor que acciona un motor donde el controlador de motor es el actuador y el motor es la planta. El motor, por tanto, gira a una velocidad determinada. El sensor conectado lee el estado actual de la planta y lo retroalimenta al microcontrolador. El microcontrolador vuelve a comparar, hace cálculos y, por tanto, el ciclo se repite. Este proceso es repetitivo e interminable por lo que el microcontrolador mantiene las condiciones deseadas

Paso 2: Sistema de control basado en PID

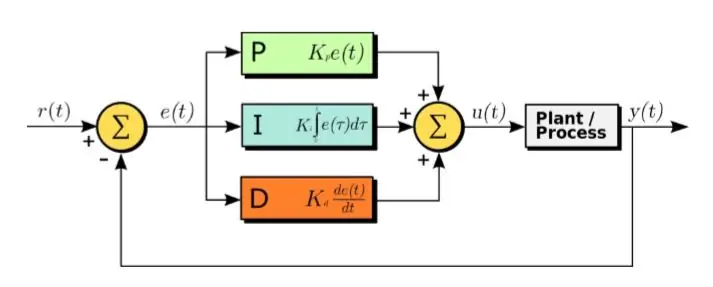
El algoritmo PID es un método eficaz para diseñar un sistema de control.

Definición

PID significa Proporcional, Integral y Derivado. En este algoritmo, la señal de error recibida es la entrada. Y la siguiente ecuación se aplica a la señal de error

U (t) = Kp ∗ e (t) + Kd ∗ d / dt (e (t)) + Ki ∗ integral (e (t)) (1.1)

Breve explicacion

Como se puede ver en la ecuación anterior, la integral y la derivada de las señales de error se calculan, se multiplican con sus respectivas constantes y se suman junto con la constante Kp multiplicada por e (t). La salida luego se alimenta al actuador que hace que el sistema funcione. Ahora veamos cada parte de la función por turno. Esta función afecta directamente el tiempo de subida, el tiempo de caída, el pico sobre el disparo, el tiempo de estabilización y el error de estado estable.

• Parte proporcional: La parte proporcional reduce el tiempo de subida y disminuye el error de estado estable. Esto significa que el sistema tardará menos en alcanzar su valor máximo y, cuando alcance su estado estable, el error de estado estable será bajo. Sin embargo, aumenta el rebasamiento del pico.

• Parte derivada: La parte derivada reduce el sobreimpulso y el tiempo de establecimiento. Esto significa que el estado transitorio del sistema será más amortiguado. Además, el sistema alcanzará su estado estable en menos tiempo. Sin embargo, no tiene ningún efecto sobre el tiempo de subida o el error de estado estable.

• Parte integral: La parte integral reduce el tiempo de subida y elimina por completo el error de estado estable. Sin embargo, aumenta el rebasamiento del pico y el tiempo de estabilización.

• Sintonización: Un buen sistema de control tendrá un tiempo de subida, un tiempo de estabilización, un exceso de pico y un error de estado estable bajos. Por lo tanto, Kp, Kd, Ki deben ajustarse con precisión para ajustar la contribución de los factores anteriores con el fin de adquirir un buen sistema de control.

Se ha adjuntado una figura que muestra el efecto de cambiar varios parámetros en el algoritmo PID.

Paso 3: Robot de equilibrio automático

Un robot autoequilibrado es un robot de dos ruedas de varias capas.

El robot intentará equilibrarse mediante la aplicación de fuerzas desiguales. Se equilibrará mediante la aplicación de una fuerza opuesta a la resultante de las fuerzas sobre el robot.

Métodos de autoequilibrio

Hay cuatro métodos de autoequilibrio de robots. Estos son los siguientes:

Autoequilibrio con dos sensores de inclinación IR

Esta es una de las formas más crudas de equilibrar el robot, ya que requiere muy menos hardware y un algoritmo relativamente sencillo. En este enfoque, se utilizan dos sensores IR inclinados para medir la distancia entre el suelo y el robot. Según la distancia calculada, el PID se puede utilizar para impulsar los motores y equilibrar el robot en consecuencia. Una desventaja de este método es que el sensor de infrarrojos puede perder algunas lecturas. Otro problema es que se requieren una interrupción y bucles para el cálculo de la distancia, lo que aumenta la complejidad temporal del algoritmo. Por tanto, este método de equilibrar el robot no es muy eficaz.

Autoequilibrio con acelerómetro

El acelerómetro nos da la aceleración del cuerpo en 3 ejes. La aceleración orientada en el eje y (hacia arriba) y el eje x (hacia adelante) nos da la medida para calcular la dirección de la gravedad y, por lo tanto, calcular el ángulo de inclinación. El ángulo se calcula de la siguiente manera:

θ = arctan (Ay / Ax) (1.2)

La desventaja de usar este método es que durante el movimiento del robot, la aceleración horizontal también se agregará a las lecturas, que es un ruido de alta frecuencia. Por tanto, el ángulo de inclinación será inexacto.

Autoequilibrio con giroscopio

Se utiliza un giroscopio para calcular las velocidades angulares a lo largo de los tres ejes. El ángulo de inclinación se obtiene mediante la siguiente ecuación.

θp (i) = θp (i − 1) + 1/6 (vali − 3 + 2vali − 2 + 2vali − 1 + vali) (1.3)

Una gran desventaja de usar el giroscopio es que tiene un pequeño sesgo de CC, que es un ruido de baja frecuencia y en poco tiempo los valores devueltos son completamente incorrectos. Esto, después de la integración, hará que el punto cero se desvíe. Como resultado de ello, el robot permanecerá en su posición vertical durante algún tiempo y se caerá una vez que llegue la deriva.

Autoequilibrio usando acelerómetro y giroscopio

Como se mencionó anteriormente, usar solo acelerómetro o giroscopio no nos dará el ángulo de inclinación correcto. Para dar cuenta de eso, se utilizan tanto el acelerómetro como el giroscopio. Ambos están integrados en MPU6050. En esto, obtenemos los datos de ambos y luego los fusionamos usando el Filtro de Kalman o el Filtro complementario.

• Filtro de Kalman: el filtro de Kalman calcula la mejor estimación del estado de un sistema dinámico a partir de mediciones ruidosas, minimizando el error cuadrático medio de la estimación. Opera en dos etapas, predicción y corrección, dadas las ecuaciones estocásticas discretas que describen la dinámica del sistema. Sin embargo, es un algoritmo muy complejo de implementar especialmente en un hardware limitado de un microcontrolador.

• Filtro complementario: este algoritmo utiliza principalmente los datos obtenidos del giroscopio y los integra a lo largo del tiempo para obtener el ángulo de inclinación. También utiliza una pequeña proporción de lecturas del acelerómetro. El filtro complementario, de hecho, minimiza el ruido de alta frecuencia del acelerómetro y el ruido de baja frecuencia del giroscopio y luego los fusiona para proporcionar el ángulo de inclinación más preciso.

Paso 4: Diseño de Robot

Hemos diseñado un robot autoequilibrado utilizando un controlador derivado proporcional implementado por filtro complementario para MPU6050. Este pequeño modelo de Robot Autoequilibrante nos ilustrará la utilidad de los Sistemas de Control en Autobalanceo de robots.

Implementación del sistema:

El sistema es un robot autoequilibrado. Se implementa mediante el controlador PID, que es un controlador derivado integral proporcional. Equilibramos el robot moviendo sus ruedas en la dirección de su caída. Al hacer eso, estamos tratando de mantener el centro de gravedad del robot por encima del punto de pivote. Para impulsar las ruedas en la dirección de su caída, debemos saber dónde está cayendo el robot y la velocidad a la que cae. Estos datos se obtienen usando MPU6050 que tiene un acelerómetro y un giroscopio. MPU6050 mide el ángulo de inclinación y da su salida al microcontrolador. El MPU6050 está interconectado con la placa STM a través de I2C. En I2C, un cable es para el reloj que se denomina SCL. El otro es para la transferencia de datos que es SDA. En esto, se utiliza la comunicación maestro-esclavo. La dirección inicial y la dirección final se especifican para saber desde dónde comienzan y dónde terminan los datos. Hemos implementado el filtro complementario aquí para MPU6050, que es un filtro matemático para fusionar las salidas del acelerómetro y el giroscopio. Después de obtener los datos del MPU6050, el microcontrolador realizará cálculos para saber dónde está cayendo. Según los cálculos, el microcontrolador STM le dará órdenes al conductor del motor para que conduzca los vehículos en la dirección de caída, lo que equilibrará el robot.

Paso 5: Componentes del proyecto

Los siguientes componentes se utilizaron en el proyecto del robot autoequilibrado:

STM32F407

Un microcontrolador diseñado por ST Microelectronics. Funciona en la arquitectura ARM Cortex-M.

Controlador de motor L298N

Este IC se utiliza para hacer funcionar el motor. Obtiene dos entradas externas. Uno del microcontrolador que le proporciona una señal PWM. Al ajustar el ancho del pulso, se puede ajustar la velocidad del motor. Su segunda entrada es la fuente de voltaje requerida para impulsar el motor, que en nuestro caso es una batería de 12V.

Motor de CC

Un motor de CC funciona con una fuente de CC. En este experimento, el motor de CC está funcionando utilizando los optoacopladores conectados al controlador del motor. Para accionar el motor hemos utilizado el Motor Drive L298N.

MPU6050

MPU6050 se utiliza para obtener información sobre dónde cae el robot. Mide el ángulo de inclinación con respecto al punto de inclinación cero que es la posición del MPU6050 cuando el programa comienza a ejecutarse.

El MPU6050 tiene un acelerómetro de 3 ejes y un giroscopio de 3 ejes. El acelerómetro mide la aceleración a lo largo de los tres ejes y el giroscopio mide la velocidad angular alrededor de los tres ejes. Para combinar la salida, debemos filtrar los ruidos de ambos. Para filtrar los ruidos, disponemos de Kalman y Filtros complementarios. Hemos implementado un filtro complementario en nuestro proyecto.

Opto Pareja 4N35

Un optoacoplador es un dispositivo que se utiliza para aislar la parte de bajo voltaje y la parte de alto voltaje del circuito. Como su nombre indica, funciona sobre la base de la luz. Cuando la parte de bajo voltaje recibe una señal, la corriente fluye en la parte de alto voltaje

Paso 6: Estructura del robot

La estructura del robot se explica a continuación:

Estructura física

El robot de autoequilibrio consta de dos capas de vidrio plástico transparente. Los detalles de dos capas se dan a continuación:

Primera capa

En la parte inferior de la primera capa, hemos colocado una celda para alimentar la placa STM. También se han colocado dos motores de 4 voltios cada uno a cada lado con neumáticos conectados para que el robot se mueva. En la parte superior de la primera capa se han colocado dos baterías de 4 voltios cada una (8 voltios en total) y un controlador de motor IC (L298N) para el funcionamiento de los motores.

Segunda capa

En la capa superior del robot, hemos colocado la placa STM en la placa Perf. Otra placa de perforación de 4 optoacopladores se coloca en la capa superior. El giroscopio también se coloca en la capa superior del robot desde el lado inferior. Ambos componentes se colocan en la parte media para que el centro de gravedad se mantenga lo más bajo posible.

Centro de gravedad del robot

El centro de gravedad se mantiene lo más bajo posible. Para ello, hemos colocado baterías pesadas en la capa inferior y componentes ligeros como placa STM y optoacopladores en la capa superior.

Paso 7: Código

El código se compiló en Atollic TrueStudio. El estudio STM se utilizó con fines de depuración.

Paso 8: Conclusión

Después de mucha experimentación y observación, finalmente llegamos al punto en que resumimos nuestros resultados y discutimos hasta qué punto logramos implementar y determinar la efectividad del sistema.

Revisión general

Durante la experimentación, la velocidad del motor se controló con éxito utilizando el algoritmo PID. Sin embargo, la curva no es exactamente una línea recta suave. Hay muchas razones para eso:

• El sensor, aunque conectado a un filtro de paso bajo, aún proporciona ciertos rebotes finitos; estos se deben a las resistencias no lineales y algunas razones inevitables de la electrónica analógica.

• El motor no gira suavemente bajo voltaje pequeño o PWM. Proporciona sacudidas que pueden causar algunos valores incorrectos alimentados al sistema.

• Debido al bamboleo, es posible que el sensor pierda algunas ranuras que proporcionan valores más altos. • Otro motivo importante de errores puede ser la frecuencia del reloj central del microcontrolador STM. Este modelo de microcontrolador STM proporciona un reloj central de 168MHz. Aunque se trató este problema en este proyecto, existe una noción general sobre este modelo de que no proporciona exactamente una frecuencia tan alta.

La velocidad de bucle abierto proporciona una línea muy suave con solo unos pocos valores inesperados. El algoritmo PID también funciona bien y proporciona un tiempo de estabilización del motor muy bajo. El algoritmo PID del motor se probó bajo varios voltajes manteniendo constante la velocidad de referencia. El cambio de voltaje no cambia la velocidad del motor mostrando que el algoritmo PID está funcionando bien

Eficacia

Aquí discutimos la efectividad del controlador PID que observamos durante la experimentación.

Implementación simple

Hemos visto en la sección de experimentación y observaciones que un controlador PID es muy fácil de implementar. Solo requiere tres parámetros o constantes que deben configurarse para tener un sistema de control de velocidad

Eficiencia inigualable para sistemas lineales

El controlador PID lineal es el más eficiente de la familia de controladores porque la lógica es muy simple y la aplicación está muy extendida en el caso de aplicaciones lineales o bastante lineales.

Limitaciones

Explicamos en resumen sobre las Limitaciones de este sistema. Aquí discutimos algunos de ellos que observamos.

Selección de constantes

Hemos visto que, aunque un controlador PID es fácil de implementar, sigue siendo un gran inconveniente del sistema que el paso de seleccionar el valor de las constantes es laborioso; ya que hay que hacer cálculos difíciles. La otra forma es el método de prueba y golpe, pero tampoco es eficiente.

Constantes no siempre constantes

Los resultados experimentales mostraron que para diferentes valores de la velocidad de referencia del motor, el controlador PID no funcionaba correctamente para los mismos valores de las constantes PID. Para diferentes velocidades, las constantes deben seleccionarse de manera diferente y esto aumenta el costo computacional exponencialmente.

No lineal

El controlador PID utilizado en nuestro caso es lineal, por lo tanto, solo se puede aplicar a sistemas lineales. Para sistemas no lineales, el controlador debe implementarse de manera diferente. Aunque se encuentran disponibles diferentes métodos no lineales de PID, requieren que se seleccionen más parámetros. Esto nuevamente hace que el sistema sea indeseable debido al alto costo computacional.

Se requiere empuje inicial

Mostramos en la sección de experimentación que para una velocidad de referencia bastante pequeña donde el error es bastante pequeño en el arranque, el PWM suministrado por el PID es tan pequeño que no genera el par de arranque requerido para el motor. Por lo tanto, el motor en algunas pruebas no funciona o en otras pruebas proporciona un gran sobreimpulso y un tiempo de estabilización más prolongado.

Paso 9: agradecimiento especial

Un agradecimiento especial a los miembros de mi grupo que me ayudaron con este proyecto.

Subiré el enlace al video pronto.

Espero que este instructivo le resulte interesante.

Este es Tahir Ul Haq de UET que se despide. Salud !!!