
Tabla de contenido:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 08:40.
- Última modificación 2025-01-23 14:39.


Aquí hay una aplicación práctica de ecuaciones matemáticas complejas.
De hecho, esta es una técnica muy útil que puede utilizar para caracterizar componentes, o incluso una antena, en frecuencias predeterminadas.
Si ha estado jugando con la electrónica, es posible que esté familiarizado con las resistencias y la ley de Ohm. R = V / I ¡Puede que ahora se sorprenda al saber que esto es todo lo que necesita para resolver las impedancias complejas también! Todas las impedancias son esencialmente complejas, es decir, tienen una parte Real e Imaginaria. En el caso de un resistor, el imaginario (o reactancia) es 0, en consecuencia, no hay diferencia de fase entre V e I, por lo que podemos dejarlos fuera.
Un resumen rápido sobre números complejos. Complejo simplemente significa que el número se compone de dos partes, una real y una imaginaria. Hay dos formas de representar números complejos, por ejemplo, en la figura anterior, un punto podría definirse por los valores Real e Imaginario, como donde se encuentran las líneas amarilla y azul. Por ejemplo, si la línea azul estuviera en 4 en el eje X y 3 en el eje Y, este número sería 4 + 3i, i indica que esta es la parte imaginaria de este número. Otra forma de definir el mismo punto sería por la longitud (o amplitud) de la línea roja, así como por el ángulo que forma con la horizontal. En el ejemplo anterior, esto sería 5 <36,87.
O una línea con una longitud de 5 en un ángulo de 36,87 grados.
En la ecuación sobre todos los parámetros, se puede pensar que R, V y yo tenemos una parte imaginaria, cuando se trabaja con resistencias, este valor es 0.
Cuando se trabaja con inductores o condensadores, o cuando se puede medir una diferencia de fase (en grados) entre señales, la ecuación sigue siendo la misma, pero se debe incluir la parte imaginaria del número. La mayoría de las calculadoras científicas facilitan mucho el trabajo con matemáticas complejas, en este tutorial trabajaré con un ejemplo en una Casio fx-9750GII.
Primero, un resumen de la ecuación del divisor de voltaje de la resistencia.
Según la figura -
El voltaje en Y es la corriente i multiplicada por R2
i es el voltaje X dividido por la suma de R1 y R2
Cuando se desconoce R2, podemos medir los otros valores, X, Y, R1 y reorganizar la ecuación para resolver R2.
Suministros
Calculadora científica
Generador de señales
Osciloscopio
Paso 1: configuración

Supongamos que queremos calcular la inductancia del dispositivo bajo prueba (DUT) a 1MHz.
El generador de señales está configurado para una salida sinusoidal de 5 V a 1 MHZ.
Estamos usando resistencias de 2k ohmios y los canales del osciloscopio son CH1 y CH2.
Paso 2: osciloscopio

Obtenemos las formas de onda como se muestra en la figura. Se puede ver y medir un cambio de fase en el osciloscopio para que tenga una ventaja de 130ns. La amplitud es de 3,4 V. Tenga en cuenta que la señal en CH1 debe ser de 2.5V ya que se toma en la salida del divisor de voltaje, aquí se muestra como 5V para mayor claridad, ya que este es el valor que también debemos usar en nuestros cálculos. es decir, 5 V es el voltaje de entrada al divisor con el componente desconocido.
Paso 3: Calcular la fase

A 1MHz, el período de la señal de entrada es 1us.
130ns da una relación de 0,13. O el 13%. 13% de 360 es 46.6
A la señal de 5V se le da un ángulo de 0.. ya que esta es nuestra señal de entrada y el desplazamiento de fase es relativo a ella.
a la señal de 3.4V se le da el ángulo de +46.6 (el + significa que está adelantado, para un capacitor el ángulo sería negativo).
Paso 4: en la calculadora


Ahora simplemente ingresamos nuestros valores medidos en la calculadora.
R es 2k
V es 5 (EDITAR - V es 5, más adelante en la ecuación se usa X! El resultado es exactamente el mismo que tengo X como 5 en mi calculadora)
Y es nuestro voltaje medido con el ángulo de fase, este número se ingresa como un número complejo, simplemente especificando el ángulo como se muestra en la pantalla de la calculadora
Paso 5: resuelve la ecuación

ahora la ecuación
(Y * R) / (X - Y)
se escribe en la calculadora, esta es exactamente la misma ecuación que usamos para resolver los divisores de voltaje de la resistencia:)
Paso 6: Valores calculados


La calculadora arrojó el resultado
18 + 1872i
El 18, es la parte real de la impedancia y tiene una inductancia de +1872 a 1MHz.
Lo que resulta en 298uH según la ecuación de impedancia del inductor.
18 ohmios es más alta que la resistencia que se mediría con un multímetro, esto se debe a que el multímetro mide la resistencia en CC. A 1MHz hay efecto piel, en el que la parte interna del conductor es desviada por la corriente y solo fluye por el exterior del cobre, disminuyendo efectivamente el área transversal del conductor y aumentando su resistencia.
Recomendado:
¡Cómo lograr cualquier resistencia / capacitancia usando componentes que ya tiene !: 6 pasos

¡Cómo lograr cualquier resistencia / capacitancia usando componentes que ya tiene !: ¡Esta no es solo otra calculadora de resistencia equivalente en serie / paralelo! Este programa calcula cómo combinar resistencias / condensadores que tiene actualmente para lograr un valor objetivo de resistencia / capacitancia que necesita. ¿Alguna vez ha necesitado una especificación?
MicroPython en la placa de sensores de artes complejas: 3 pasos

MicroPython en la placa de sensores de artes complejas: uno de los aspectos más sorprendentes del microcontrolador ESP32 es su capacidad para ejecutar MicroPython. Esto se puede hacer de dos formas: ejecutando programas completos de Python o de forma interactiva a través de una aplicación de consola. Este Instructable demostrará cómo usar
Reloj arcoíris de matemáticas y física: 3 pasos (con imágenes)
Reloj Arco Iris de Matemáticas-Física: Hace un tiempo tuve la idea de crear mi propio reloj de Física / Matemáticas, así que comencé a diseñarlo en Inkscape. Cada hora, de 1 a 12, reemplacé con fórmula de Física / Matemáticas: 1 - Ecuación de Euler2 - Integral 3 - Función trigonométrica4 - Integral de trigonom
Generación de tonos de diferentes tipos usando ecuaciones matemáticas (MathsMusic) Arduino: 5 pasos

Generación de tonos de diferentes tipos usando ecuaciones matemáticas (MathsMusic) Arduino: Descripción del proyecto: Ha comenzado un nuevo viaje donde las ideas se pueden implementar fácilmente utilizando la comunidad de código abierto (gracias a Arduino). Así que aquí hay una manera · Mire a su alrededor y observe su entorno · Descubra los problemas que deben ser
Análisis de impedancia biológica (BIA) con el AD5933: 9 pasos
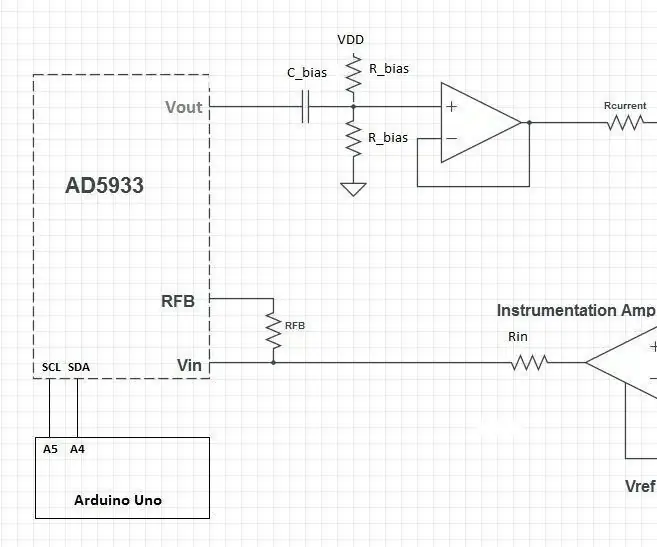
Análisis de impedancia biológica (BIA) con el AD5933: me ha interesado hacer un analizador de impedancia biológica para las mediciones de la composición corporal y mis búsquedas aleatorias siguieron encontrando un diseño de la clase de instrumentación biomédica de 2015 en la Universidad de Vanderbilt. He trabajado en el diseño y estoy
