Resolver tablas de verdad: 10 pasos

2024 Autor: John Day | [email protected]. Última modificación: 2024-01-30 08:40

Una tabla de verdad es una forma de visualizar todos los resultados de un problema. Este conjunto de instrucciones está hecho para personas que se inician en matemáticas discretas. Practicaremos hoy con un problema de ejemplo que es específico de estas instrucciones. Necesitará un papel borrador y un lápiz para visualizar la mesa. Este problema debería tardar unos 5 minutos en completarse para las personas con conocimientos previos sobre el tema y unos 10 minutos para los principiantes.

Para este conjunto de instrucciones, nos centraremos en el problema ~ p Λ q. Estamos usando esto para introducir algunos símbolos necesarios para interpretar tablas de verdad.

Paso 1: Comprensión de las tablas de verdad

Una tabla de verdad es una forma de visualizar todas las posibilidades de un problema. Conocer las tablas de verdad es una necesidad básica para las matemáticas discretas. Aquí, encontraremos todos los resultados de la ecuación simple de ~ p Λ q.

Paso 2: Conocer los símbolos

El primer paso hacia la tabla de la verdad es comprender las señales. El “~” en este problema particular significa negación. La "p" y la "q" son ambas variables. El "Λ" es equivalente a "y". Esta ecuación se lee como “no p y q”, lo que significa que la ecuación es verdadera si p no es verdadera y q es verdadera.

Paso 3: formatear la tabla

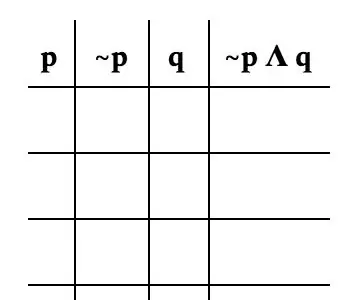
Ahora para formar la tabla real. Es importante dividir el problema por cada variable. Para este problema, lo dividiremos de la siguiente manera: p, ~ p, q y ~ p Λ q. La imagen es un buen ejemplo de cómo debería verse su mesa.

Paso 4: Asignación de verdadero y falso

Dado que solo hay dos variables, solo habrá cuatro posibilidades por variable. Para p, lo dividimos con la mitad de los espacios ocupados por T (para verdadero) y la otra mitad por F (para falso).

Paso 5: Negación

Para ~ p, escribe el signo opuesto que tiene p, ya que ~ p es el opuesto de p.

Paso 6: Variable "q"

Para q, alterna entre T y F para obtener cada combinación posible. Dado que la ecuación solo se enfoca en ~ p, podemos ignorar la columna p al determinar la verdad de la ecuación. El símbolo “Λ” significa que tanto ~ pyq deben ser verdaderas para que la ecuación sea verdadera.

Paso 7: resolver el falso en la última columna

Para la primera fila, dado que ~ p es F yq es T, ~ p Λ q es F en el escenario en el que ~ p es F yq es T. El único escenario en el que la ecuación es T es donde ~ p es T y q es T.

Paso 8: Encontrar lo verdadero en la última columna

Esto significa que la única fila que es T es la tercera.

Paso 9: terminar la mesa

Verifique que su tabla sea correcta. Para hacer esto, verifique que sus letreros sean correctos y asegúrese de que la última columna esté hecha correctamente. La última columna es el resultado de todas las posibles permutaciones de las variables.

Paso 10: Listo

Ahora que sabes cómo hacer una tabla de verdad básica, ¡sigue practicando! Cuanto más practique, mejor lo hará.