Báscula digital con ESP32: 12 pasos

2024 Autor: John Day | [email protected]. Última modificación: 2024-01-30 08:43

¿Alguna vez pensó en montar una báscula digital usando un ESP32 y un sensor (conocido como celda de carga)? Hoy te mostraré cómo hacer esto a través de un proceso que también permite otras pruebas de laboratorio, como identificar la fuerza que realiza un motor en un punto, entre otros ejemplos.

Luego demostraré algunos conceptos relacionados con el uso de celdas de carga, capturaré datos de celdas para construir una báscula de ejemplo y señalaré otras posibles aplicaciones de las celdas de carga.

Paso 1: Recursos utilizados

• Heltec Lora 32 WiFi ESP

• Celda de carga (0 a 50 newtons, usando una báscula)

• 1 potenciómetro de 100k (mejor si usa un potenciómetro multivoltio para un ajuste fino)

• 1 amperio Op LM358

• 2 resistencias de 1M5

• 2 resistencias de 10k

• 1 resistencia de 4k7

• Alambres

• Un protoboard

• Un cable USB para ESP

• Una báscula, recipiente con volumen graduado o cualquier otro método de calibración.

Paso 2: demostración

Paso 3: Celdas de carga

• Son transductores de fuerza.

• Pueden usar varios métodos para traducir la fuerza aplicada en una magnitud proporcional que se puede usar como medida. Entre los más habituales se encuentran los que utilizan extensómetros de chapa, EL efecto piezoeléctrico, hidráulicos, cuerdas vibrantes, etc…

• También se pueden clasificar por la forma de medición (tensión o compresión)

Paso 4: Celdas de carga y galgas extensiométricas

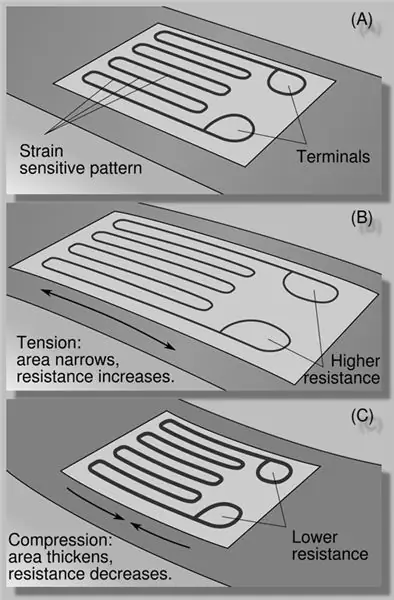
• Los extensómetros de láminas son películas (generalmente de plástico) con un alambre impreso que tienen una resistencia que puede variar con su cambio de tamaño.

• Su construcción tiene como objetivo principal convertir una deformación mecánica en una variación de magnitud eléctrica (resistencia). Esto ocurre preferiblemente en una sola dirección, de modo que se pueda realizar la evaluación de componentes. Para ello es habitual la combinación de varios extensómetros

• Cuando se fija correctamente a un cuerpo, su deformación es igual a la del cuerpo. Así, su resistencia varía con la deformación del cuerpo, que a su vez está relacionada con la fuerza deformante.

• También se conocen como galgas extensométricas.

• Cuando se estira mediante una fuerza de tracción, las hebras se alargan y estrechan, aumentando la resistencia.

• Cuando se comprime por una fuerza de compresión, los cables se acortan y ensanchan, reduciendo la resistencia.

Paso 5: Puente de Wheatstone

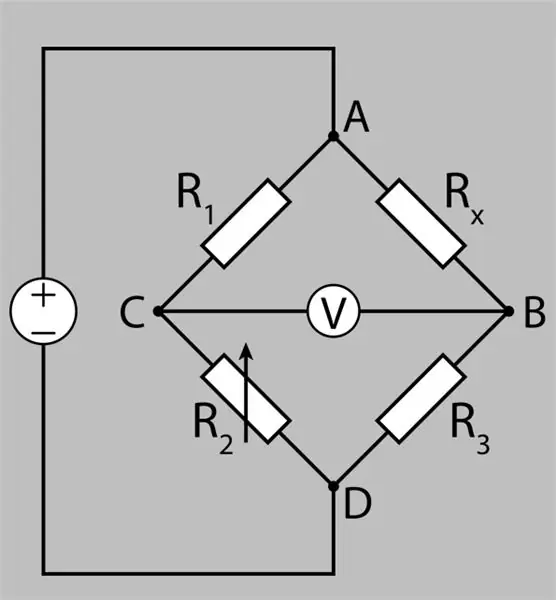
• Para una medición más precisa y para permitir una detección más eficiente de la variación de resistencia en una celda de carga, la galga extensométrica se ensambla en un puente de Wheatstone.

• En esta configuración, podemos determinar la variación de la resistencia a través del desequilibrio del puente.

• Si R1 = Rx y R2 = R3, los divisores de voltaje serán iguales y los voltajes Vc y Vb también serán iguales, con el puente en equilibrio. Es decir, Vbc = 0V;

• Si Rx es diferente a R1, el puente estará desequilibrado y el voltaje Vbc será distinto de cero.

• Es posible mostrar cómo debe ocurrir esta variación, pero aquí realizaremos una calibración directa, relacionando el valor leído en el ADC con una masa aplicada a la celda de carga.

Paso 6: amplificación

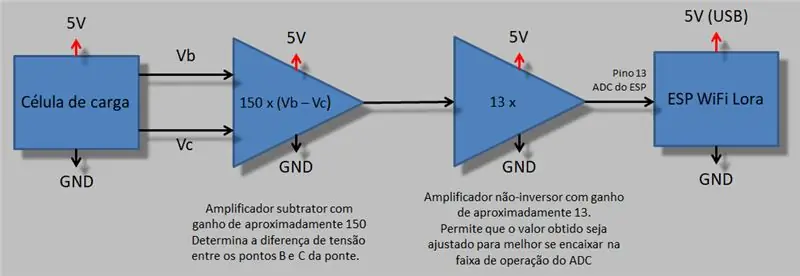
• Incluso usando el puente de Wheatstone para hacer la lectura más eficiente, las microdeformaciones en el metal de la celda de carga producen pequeñas variaciones de voltaje entre Vbc.

• Para solucionar esta situación, utilizaremos dos etapas de amplificación. Uno para determinar la diferencia y otro para igualar el valor obtenido con el ADC del ESP.

Paso 7: Amplificación (esquema)

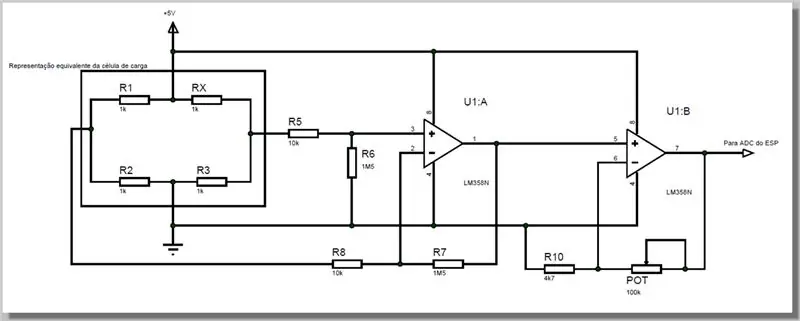
• La ganancia del paso de resta viene dada por R6 / R5 y es la misma que R7 / R8.

• La ganancia del paso final no inversor viene dada por Pot / R10

Paso 8: recopilación de datos para la calibración

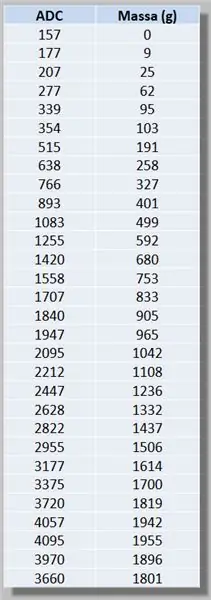
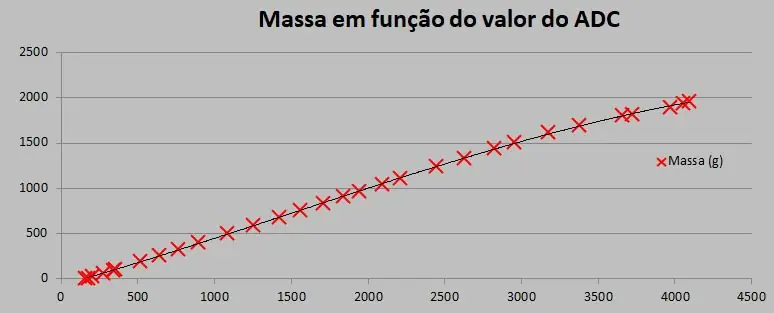
• Una vez ensamblado, establecemos la ganancia final de modo que el valor de la mayor masa medida esté cerca del valor máximo del ADC. En este caso, por 2 kg aplicados en la celda, el voltaje de salida fue de alrededor de 3V3.

• A continuación, variamos la masa aplicada (conocida a través de una balanza y para cada valor), y asociamos un LEITUR del ADC, obteniendo la siguiente tabla.

Paso 9: Obtención de la relación de funciones entre la masa medida y el valor del ADC obtenido

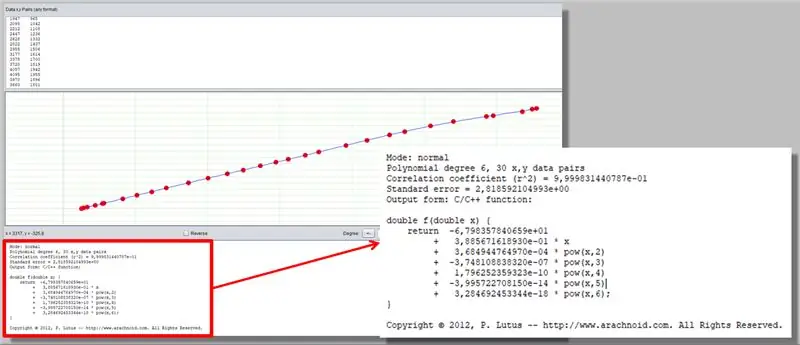
Usamos el software PolySolve para obtener un polinomio que representa la relación entre la masa y el valor del ADC.

Paso 10: código fuente

Código fuente - #Incluye

Ahora que sabemos cómo obtener las medidas y conocemos la relación entre el ADC y la masa aplicada, podemos pasar a escribir el software.

// Bibliotecas para utilização do display oLED # include // Necesario apenas para o Arduino 1.6.5 e anterior #include "SSD1306.h" // o mesmo que #include "SSD1306Wire.h"

Código fuente - #Defines

// Os pinos do OLED están conectados ao ESP32 pelos seguintes GPIO's: // OLED_SDA - GPIO4 // OLED_SCL - GPIO15 // OLED_RST - GPIO16 #define SDA 4 #define SCL 15 #define RST 16 // RST deve ser por software

Fuente: variables y constantes globales

Pantalla SSD1306 (0x3c, SDA, SCL, RST); // Instanciando y ajustando los pinos del objeto "display" const int amostras = 10000; // número de amostras coletadas para a média const int pin = 13; // pino de leitura

Código fuente - Configuración ()

configuración vacía () {pinMode (pin, ENTRADA); // pino de leitura analógica Serial.begin (115200); // iniciando una serie // Inicia o display display.init (); display.flipScreenVertically (); // Vira a tela verticalmente}

Código fuente - Bucle ()

void loop () {float medidas = 0.0; // variável para manipular as medidas float massa = 0.0; // variável para armazenar o valor da massa // inicia a coleta de amostras do ADC for (int i = 0; i (5000)) // se está ligado a mais que 5 segundos {// Envia um CSV contendo o instant, a medida média do ADC e o valor em gramas // para a Serial. Serial.print (millis () / 1000.0, 0); // instante en segundos Serial.print (","); Serial.print (medidas, 3); // valor médio obtido no ADC Serial.print (","); Serial.println ((massa), 1); // massa em gramas // No guardar búfer do display display.clear (); // Limpa o buffer do display // ajusta o alinhamento para a esquerda display.setTextAlignment (TEXT_ALIGN_LEFT); // ajusta una fuente para Arial 16 display.setFont (ArialMT_Plain_16); // No guardar búfer muestra una pantalla massa.drawString (0, 0, "Massa:" + String (int (massa)) + "g"); // no guardar búfer o valor para ADC display.drawString (0, 30, "ADC:" + String (int (medidas))); } else // se está ligado a menos de 5 segundos {display.clear (); // limpa o búfer mostrar display.setTextAlignment (TEXT_ALIGN_LEFT); // Ajusta o alinhamento para a esquerda display.setFont (ArialMT_Plain_24); // ajusta una fuente para Arial 24 display.drawString (0, 0, "Balança"); // eliminar sin búfer display.setFont (ArialMT_Plain_16); // Ajusta una fuente para Arial 16 display.drawString (0, 26, "ESP-WiFi-Lora"); // eliminar no búfer} display.display (); // transferir o búfer para o mostrar retraso (50); }

Código fuente - Función calculaMassa ()

// função para cálculo da massa obtida pela regressão // usando oPolySolve float calculaMassa (float medida) {return -6.798357840659e + 01 + 3.885671618930e-01 * medida + 3.684944764970e-04 * medida * medida + -3.748108838320e-07 * medida * medida * medida + 1.796252359323e-10 * medida * medida * medida * medida + -3.995722708150e-14 * medida * medida * medida * medida * medida + 3.284692453344e-18 * medida * medida * medida * medida * medida * medida; }

Paso 11: Iniciar y medir

Paso 12: Archivos

Descarga los archivos

INO

PDF