Suma recursiva de una matriz en Java: 9 pasos

2025 Autor: John Day | [email protected]. Última modificación: 2025-01-13 06:57

La recursividad es un procedimiento muy útil y eficiente en el tiempo que puede resolver rápidamente un problema con muy poco código. La recursividad involucra el método que usted crea llamándose a sí mismo acortando el problema original.

Para este ejemplo, sumaremos una matriz de 10 enteros, pero el tamaño podría tener cualquier longitud.

Suministros

Debe conocer la sintaxis básica de Java y tener su IDE o un editor de texto para escribir su código para esta tarea.

Paso 1: Configure su método principal

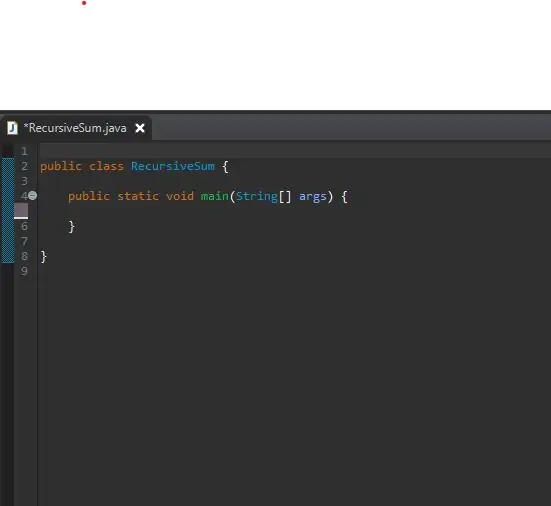
Para comenzar, configure su método principal en una clase recién creada. He nombrado a mi clase RecursiveSum. Aquí es donde creará la matriz de enteros y llamará a su método recursivo.

Paso 2: Crea tu encabezado de método recursivo

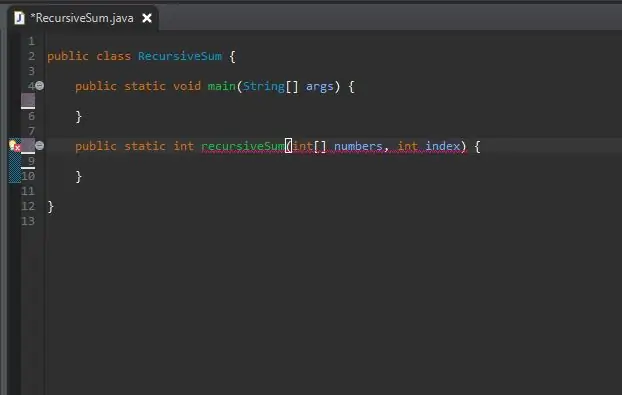
Fuera de su método principal, cree el encabezado del método para su método recursivo.

El método es estático, ya que no requerirá un objeto para usarlo.

El tipo de retorno es int, ya que la matriz que usaremos estará llena de enteros. Sin embargo, esto se puede cambiar a cualquier tipo de número que contenga la matriz.

He nombrado mi método recursiveSum que tomará dos parámetros; una matriz de enteros y el índice que agregaremos a la suma. He llamado a estos parámetros números e índice respectivamente.

Verá errores ahora mismo y eso está bien. Se solucionarán más adelante.

Paso 3: Crea tu Kicker / caso base

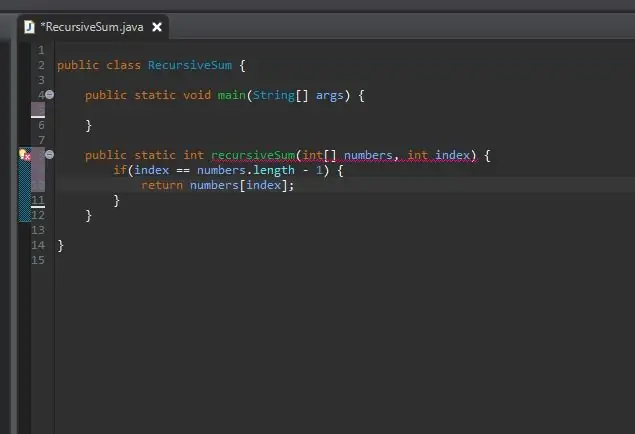
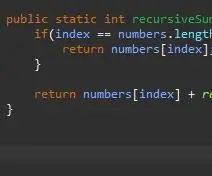
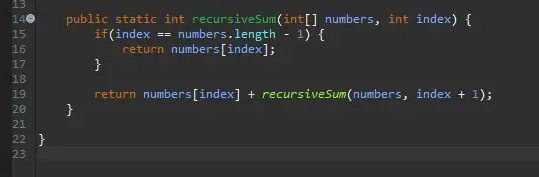
Un método recursivo necesita un caso base / kicker. Esta es la condición que evitará que su método se llame a sí mismo infinitamente. Este caso base puede pensarse como el caso más simple que encontraremos. En este caso, el caso base será cuando estemos al final de nuestra matriz. Si el índice actual es igual a la longitud de la matriz (menos 1 porque las matrices comienzan a contar desde 0, no 1), estamos al final y simplemente devolvemos ese elemento en ese índice.

Paso 4: el paso recursivo

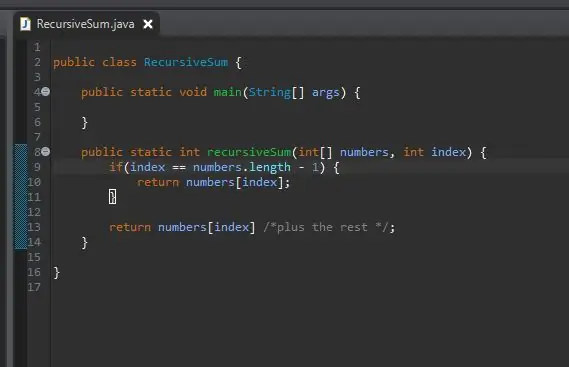
Una vez que tenemos nuestro caso base, el siguiente paso es nuestro paso recursivo. Aquí es donde ocurre la magia. Hemos manejado el caso cuando nuestro índice es igual al último elemento de nuestra matriz. ¿Qué pasa si no estamos en el último elemento de nuestra matriz? ¿Qué pasaría si pudiéramos simplemente decirle que agregue nuestro elemento actual más el siguiente? Eventualmente llegaremos al final de nuestra matriz y nuestro caso base tendrá efecto.

Para lograr esto, simplemente devolvemos nuestro índice actual y "agregamos el resto" de la matriz.

Paso 5: acorte el problema

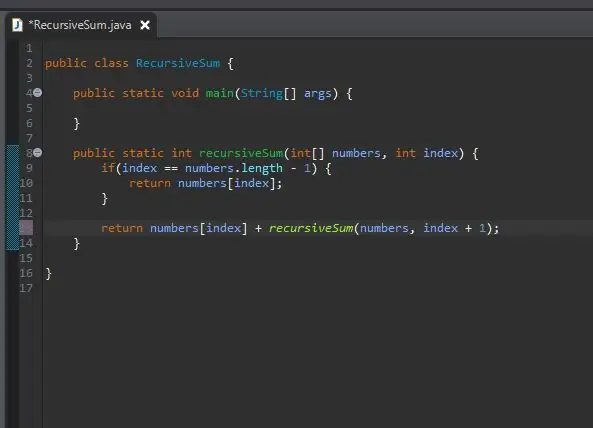
¿Cómo simplemente "sumamos el resto"? Ya tenemos un método que agregará un determinado elemento; nuestro método recursiveSum ()! Podemos llamarlo de nuevo, pero cambiamos el índice que estamos sumando.

Pasamos la misma matriz que estamos procesando, pero pasamos el siguiente índice de nuestro índice actual. Hacemos esto simplemente agregando uno a nuestro índice actual como se muestra.

Paso 6: crea la matriz de números enteros

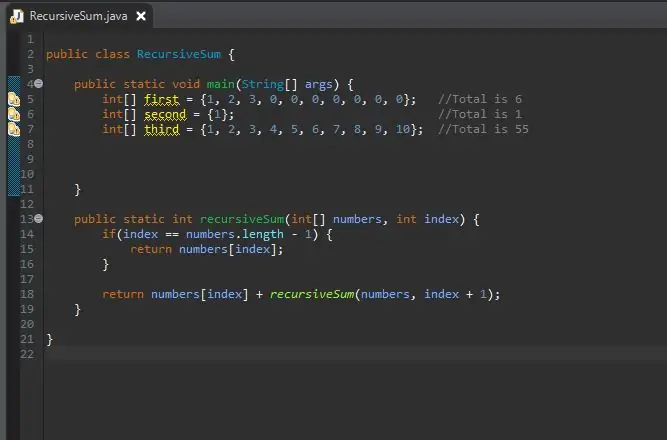
Ahora que nuestro método de suma recursivo está completo, podemos crear nuestra matriz que procesaremos. Esta matriz estará en nuestro bloque de método principal.

Puede hacer que el tamaño de la matriz sea tan largo como desee. He creado algunas matrices diferentes con diferentes tamaños y valores para mostrar que funciona no solo en un tamaño único.

Paso 7: Llame al método con sus matrices

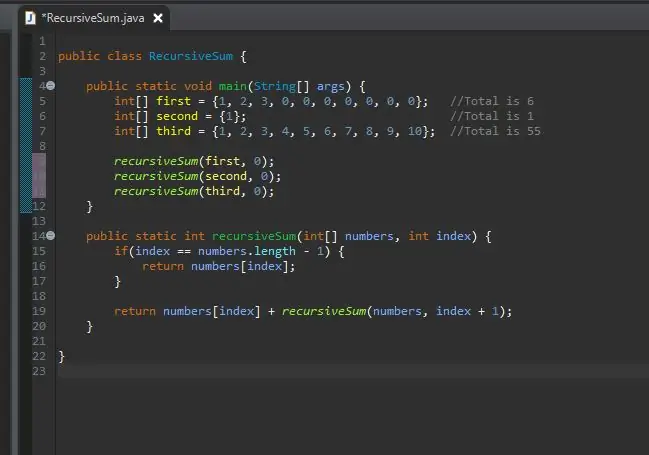
Ahora puede llamar a su método recursivo y pasarle estas matrices. Ahora puede ejecutar su programa.

Paso 8: imprima los resultados

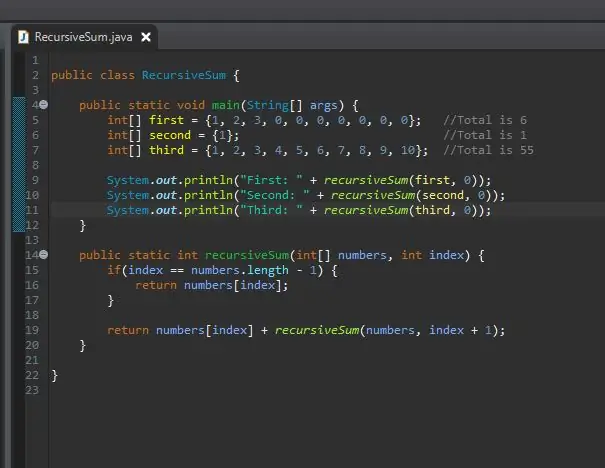
No pasó nada. ¿Por qué? La suma recursiva devuelve un número entero, pero no hemos hecho nada con este número entero. Hizo su trabajo pero no podemos ver el resultado. Para ver el resultado, simplemente lo imprimimos así. Después de ejecutar esto, debería ver los resultados para cada una de sus matrices.

Paso 9: Felicitaciones

Has completado una función recursiva. No dude en cambiar el tamaño de sus matrices. Si lo prueba, notará que falla cuando tiene una matriz vacía. No lo hemos tenido en cuenta, pero es una excelente manera de mejorar su método recursivo.