
Tabla de contenido:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 08:43.
- Última modificación 2025-01-23 14:40.
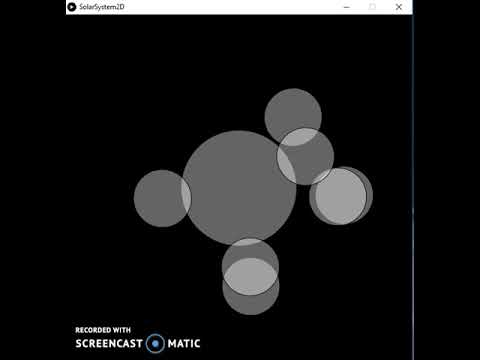
Para este proyecto, me propuse crear una simulación de cómo la gravedad afecta el movimiento de los cuerpos planetarios en un sistema solar. En el video de arriba, el cuerpo del Sol está representado por la esfera de malla de alambre y los planetas se generan aleatoriamente.
El movimiento de los planetas se basa en la física real, la Ley de Gravitación Universal. Esta ley define la fuerza gravitacional ejercida sobre una masa por otra masa; en este caso, el Sol en todos los planetas, y los planetas entre sí.
Para este proyecto utilicé Processing, un entorno de programación basado en Java. También utilicé el archivo de ejemplo de Processing que simula la gravedad de los planetas. Todo lo que necesita para esto es el software de procesamiento y una computadora.
Paso 1: simulación bidimensional

Comencé viendo algunos videos sobre cómo codificar esto que Dan Shiffman creó en su canal de YouTube, Coding Train (Parte 1/3). En este punto, pensé que usaría la recursividad para generar el sistema solar, de manera similar a como lo hace Shiffman solo usando las leyes de la física.
Creé un objeto de planeta que tenía 'planetas niños', que a su vez también tenían planetas 'niños'. El código para la simulación 2D no estaba terminado porque no tenía una buena forma de simular las fuerzas gravitacionales de cada planeta. Partí de esta forma de pensar, en una dirección basada en el ejemplo de procesamiento incorporado de la atracción gravitacional. El problema era que necesitaba calcular la fuerza gravitacional de todos los demás planetas de cada planeta, pero no podía pensar en cómo extraer fácilmente la información de un planeta individual. Después de ver cómo lo hace el tutorial de procesamiento, me di cuenta exactamente de cómo hacerlo usando bucles y matrices.
Paso 2: llevarlo a 3 dimensiones

Usando el código de ejemplo para Atracción planetaria que viene con el procesamiento, comencé un nuevo programa para una simulación 3D. La principal diferencia está en la clase Planeta, donde agregué una función de atracción, que calcula la fuerza gravitacional entre dos planetas. Esto me permitió simular cómo funciona nuestro sistema solar, donde los planetas no solo se sienten atraídos por el sol, sino también por todos los demás planetas.
Cada planeta tiene características generadas aleatoriamente como la masa, radio, velocidad orbital inicial, etc. Los planetas son esferas sólidas y el Sol es una esfera de malla de alambre. Además, la ubicación de la cámara gira alrededor del centro de la ventana.
Paso 3: uso de planetas reales

Después de que obtuve el marco para la simulación 3D, usé Wikipedia para encontrar los datos planetarios reales de nuestro sistema solar. Creé una serie de objetos planetarios e ingresé los datos reales. Cuando hice esto, tuve que reducir todas las características. Cuando hice esto, debería haber tomado los valores reales y multiplicarlos por un factor para reducir los valores, en lugar de eso, lo hice en unidades de Tierras. Es decir, tomé la relación entre el valor de la Tierra y el valor de los otros objetos, por ejemplo, el Sol tiene 109 veces más masa que la Tierra. Sin embargo, esto dio como resultado que los tamaños de los planetas parecieran demasiado grandes o demasiado pequeños.
Paso 4: Pensamientos y comentarios finales
Si continuara trabajando en esta simulación, refinaría / mejoraría un par de cosas:
1. Primero, escalaría todo de manera uniforme usando el mismo factor de escala. Luego, para mejorar la visibilidad de las órbitas, agregaría un rastro detrás de cada planeta para ver cómo se compara cada revolución con la anterior.
2. La cámara no es interactiva, lo que significa que parte de las órbitas están fuera de la pantalla, "detrás de la persona". Existe una biblioteca de cámaras 3D llamada Peazy Cam, que se utiliza en la Parte 2 de la serie de videos de Coding Train sobre este tema. Esta biblioteca permite al espectador rotar, desplazar y acercar la cámara para poder seguir la órbita completa de un planeta.
3. Finalmente, los planetas son actualmente indistinguibles entre sí. Me gustaría agregar 'pieles' a cada planeta y al Sol, para que los espectadores puedan reconocer la Tierra y demás.
Recomendado:
Cómo hacer un registrador de datos en tiempo real de humedad y temperatura con Arduino UNO y tarjeta SD - Simulación del registrador de datos DHT11 en Proteus: 5 pasos
Cómo hacer un registrador de datos en tiempo real de humedad y temperatura con Arduino UNO y tarjeta SD | Simulación del registrador de datos DHT11 en Proteus: Introducción: hola, soy Liono Maker, aquí está el enlace de YouTube. Estamos haciendo un proyecto creativo con Arduino y trabajamos en sistemas embebidos. Data-Logger: Un registrador de datos (también registrador de datos o registrador de datos) es un dispositivo electrónico que registra datos a lo largo del tiempo w
Autodesk Tinkercad Simulación del juego Arduino UNO Ping Pong V2.0 :: 5 pasos
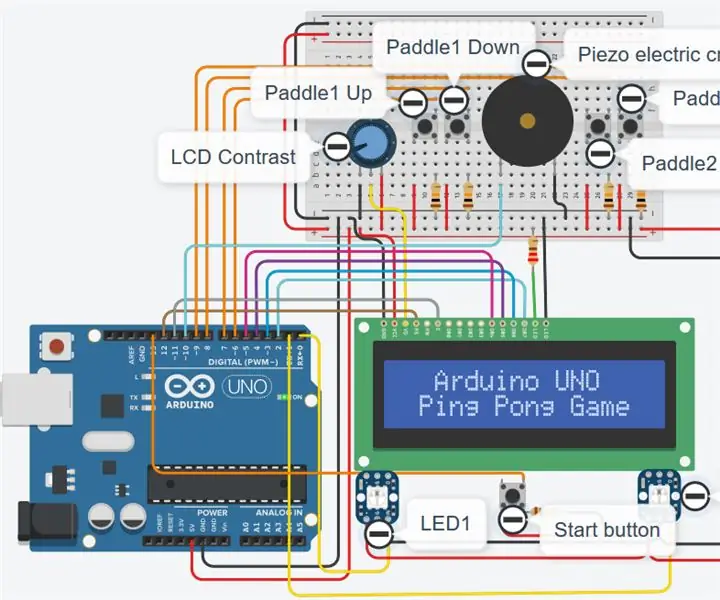
Autodesk Tinkercad Simulación de Arduino UNO Ping Pong Game V2.0 :: Hola chicos, en este instructivo aprenderán a simular ping pong en el sitio web de Autodesk Tikercad usando la placa de desarrollo Arduino UNO. Haga clic en este enlace de YouTube para ver el video de simulación
INSTALACIÓN DE REEMPLAZO DEL BOTÓN TRASERO DEL BOTÓN TRASERO DEL CERRADURA DEL PORTÓN TRASERO DE RENAULT SCENIC / MEGANE: 3 Pasos

INSTALACIÓN DE REEMPLAZO DEL BOTÓN TRASERO DEL BOTÓN DE LA PUERTA TRASERA DE RENAULT SCENIC / MEGANE: La junta tórica de mala calidad que mantiene el botón del maletero en su lugar se desgasta y se pierde el botón del maletero del vehículo. La única solución de Renaults para esto es un mecanismo de bloqueo de arranque de reemplazo completo que solo fallará nuevamente y costará
Simulación del diseño de circuitos + PCB en Proteus: 10 pasos
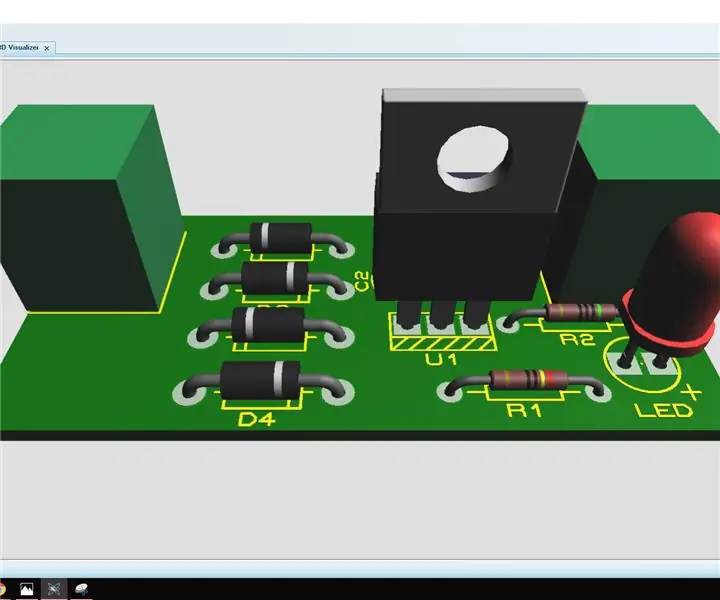
Simulación del diseño de circuitos + PCB en Proteus: este es un paso a paso instructivo para ingenieros y aficionados. En este instructable discutiré sobre simulaciones de circuitos & Diseño de PCB en Proteus 8, al final también hablaré sobre el grabado de circuitos eléctricos en 5 minutos. Con t
Interfaz del microcontrolador 8051 con 16 * 2 Lcd en la simulación de Proteus: 5 pasos (con imágenes)
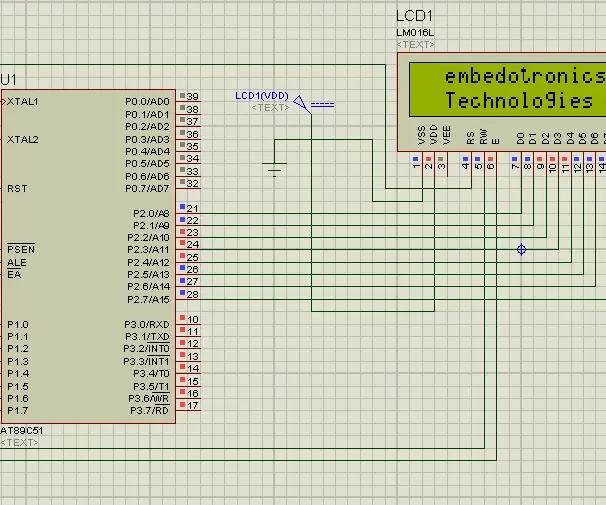
Interfaz del microcontrolador 8051 con 16 * 2 Lcd en la simulación de Proteus: Este es un proyecto muy básico del 8051. En este proyecto vamos a contarle cómo podemos interconectar 16 * 2 lcd con el microcontrolador 8051. Entonces aquí estamos usando el modo completo de 8 bits. En el siguiente tutorial también hablaremos sobre el modo de 4 bits
