¿Conoce el ajuste ESP32 ADC ?: 29 pasos

2024 Autor: John Day | [email protected]. Última modificación: 2024-01-30 08:42

Hoy, voy a hablar sobre un problema más técnico, pero creo que todos los que trabajan con ESP32 deberían saber: el problema del ajuste de lectura de ADC (convertidor analógico a digital). Encuentro esto importante porque cuando se hace una "medición", especialmente con un instrumento que tiene una salida analógica, debe estar absolutamente seguro de que la lectura se está realizando correctamente.

En el video de hoy, por lo tanto, realizaremos mediciones utilizando el "convertidor analógico-digital" del ESP32, observaremos las discrepancias de conversión y aplicaremos un método de ajuste / calibración ADC.

Paso 1: ¿Qué es un convertidor AD?

Un convertidor AD es un circuito capaz de traducir una cantidad analógica (continua) en valores digitales (discretos). ¿Qué significa eso? Significa que mientras que los valores digitales solo pueden asumir valores discretos formados por la combinación de ceros y unos, una cantidad analógica puede asumir cualquier valor dentro de un rango. Por ejemplo, si medimos el voltaje de una celda AA ideal, podríamos encontrar cualquier valor entre 0V y 1.5V, ya que esta es una cantidad analógica. El estado de salida de una lámpara ideal debe asumir solo dos estados (apagado o encendido), que es una magnitud discreta. Dado que los microcontroladores funcionan utilizando esta lógica discreta, necesitamos un circuito capaz de convertir una cantidad analógica en digital (o discreta).

Paso 2: Recursos utilizados

• Una tarjeta Lolin32 Lite v1.0.0

• Un osciloscopio Tektronix TDS1001C para capturar

• Un cable USB para el ESP32

• Un osciloscopio Hantek DSO4102C como generador de señales

Paso 3: ESP32 ADC

Según los datos de Espressif, los chips ESP32 pueden presentar una diferencia de +/- 6% de un chip a otro en los resultados medidos.

Además, la conversión NO tiene una respuesta lineal para cada rango disponible para lectura. Espressif proporciona un método de calibración y sugiere que los usuarios implementen otros métodos si lo consideran necesario para lograr la precisión deseada.

Realizaremos una adquisición de datos, y a partir de esto, mostraremos las respuestas de ADC y un ejemplo de aplicación de un proceso matemático para leer el ajuste.

Hay varias formas (más simples o más complejas) de lograr estas correcciones. Depende de ti evaluar el más adecuado para tu proyecto.

El que se muestra aquí tendrá un propósito ilustrativo y tratará de abordar puntos interesantes que se pueden observar durante los ajustes.

Paso 4: circuito utilizado

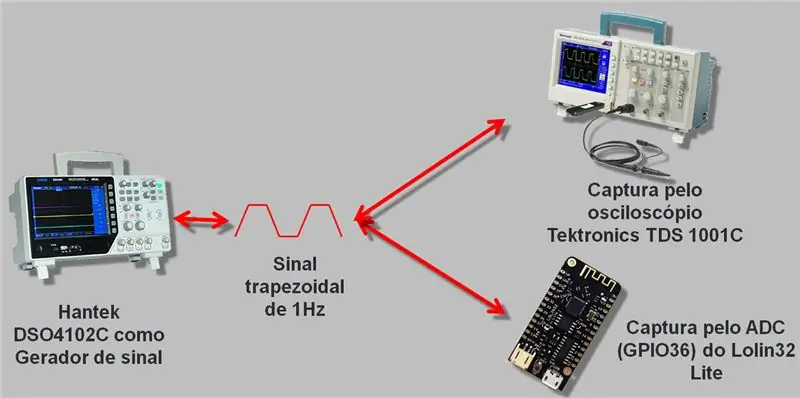
Usé un osciloscopio con un generador de señal que llega hasta los 25 MHz, el Hantek DSO4102C. Generamos una onda que fue leída por el ESP A / D y el osciloscopio. Los datos recolectados fueron registrados en csv y en una hoja de cálculo, que dejaré al final del artículo para su descarga.

Paso 5: Señal utilizada

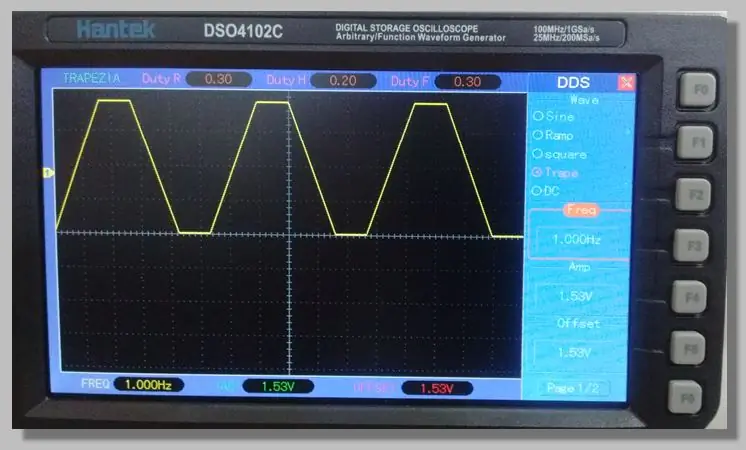
Elegimos una señal trapezoidal de baja frecuencia que permite el acceso a las rampas que recorren todo el rango de conversión. Esto permite una gran cantidad de muestras en estas rampas.

Paso 6: datos obtenidos por el osciloscopio

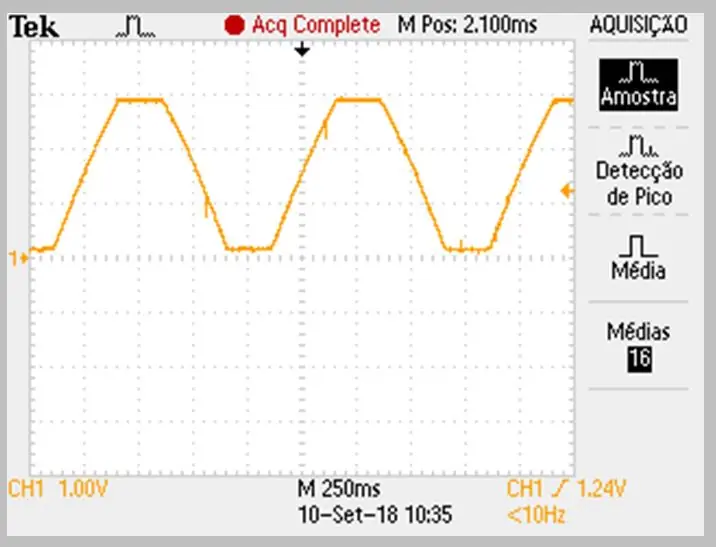
La imagen de la captura fue realizada por el osciloscopio. Los datos se almacenaron en un archivo csv. Note la ligera curvatura en las rampas ascendentes y descendentes de la señal.

Paso 7: Datos obtenidos por el osciloscopio (archivo csv en Excel)

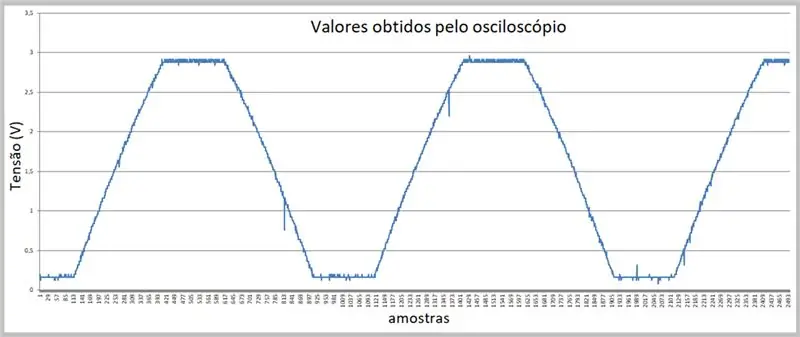
Tenemos las muestras aquí.

Paso 8: datos obtenidos por el ADC

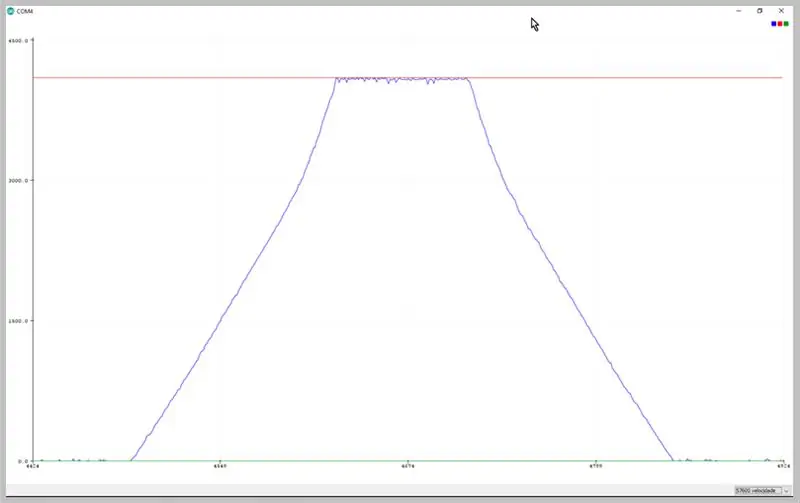
Al cambiar la tasa de transferencia del serial, podemos ver los datos capturados por el ADC. Observe la deformación de la señal trapezoidal.

Datos observados en el trazador serial Arduino IDE

Paso 9: Datos obtenidos por ADC - Excel

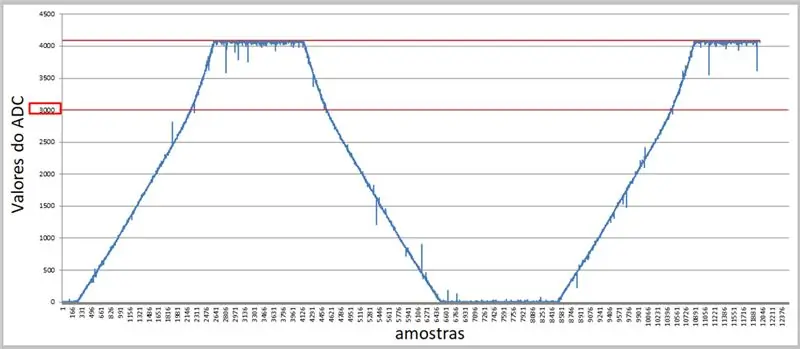
Usando una tasa más alta y el terminal serial, podemos capturar los valores y aplicarlos en Excel para nuestras comparaciones.

Paso 10: Comparación de rampas de ascenso

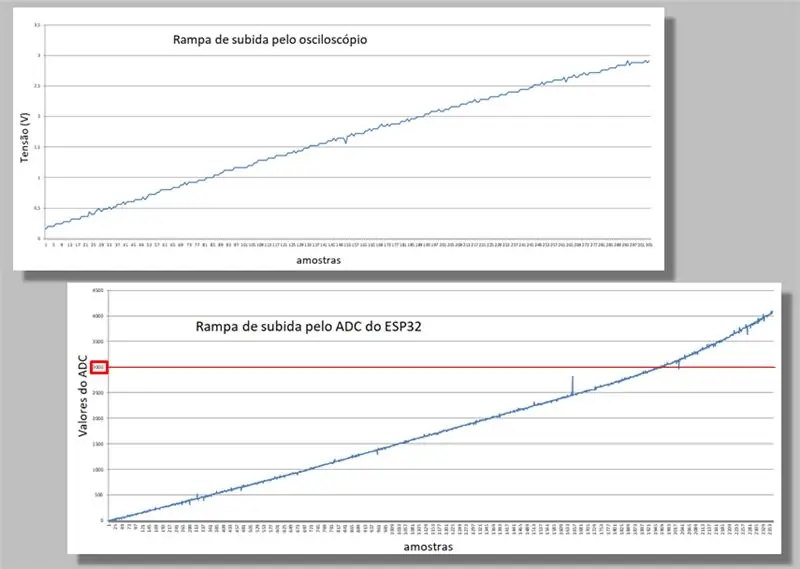
Comparamos las dos rampas de ascenso de las dos capturas.

Tenga en cuenta la curvatura que se produce en ambas rampas.

Tenga en cuenta también que para la misma rampa, tenemos muchas más muestras del ESP32 que del osciloscopio.

Paso 11: igualar el número de muestras

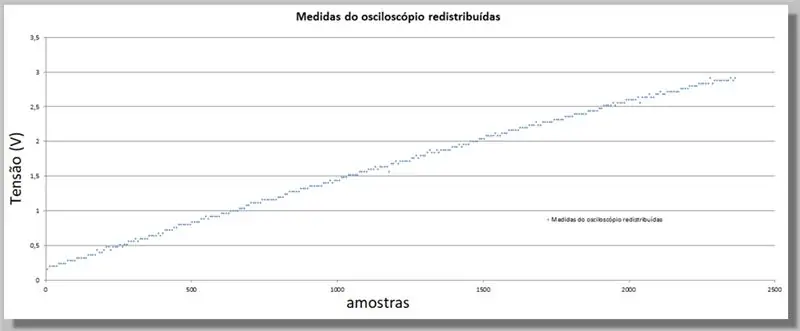
Debido a que el ESP32 proporcionó una mayor cantidad de muestras que el osciloscopio, necesitamos igualar estos valores, ya que servirán como índice para comparar las dos curvas.

Para ello, haremos una comparación directa.

Tenemos 305 muestras para la rampa del osciloscopio y 2365 muestras para la rampa ADC.

Dado que las rampas son del mismo rango, podemos decir que tenemos aproximadamente 7.75 muestras del ADC para cada osciloscopio.

Multiplicar el índice de cada muestra de osciloscopio tiene la misma curva, pero con índices equivalentes al ADC y los datos redistribuidos.

Para completar los datos faltantes para las nuevas posiciones, aplicaremos una curva que se ajuste estadísticamente a los datos conocidos.

Paso 12: Llenando los vacíos - Línea de tendencia

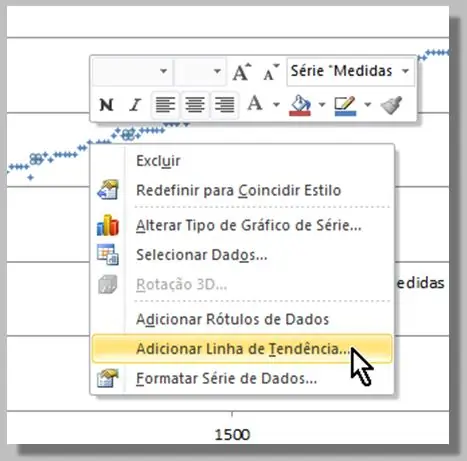
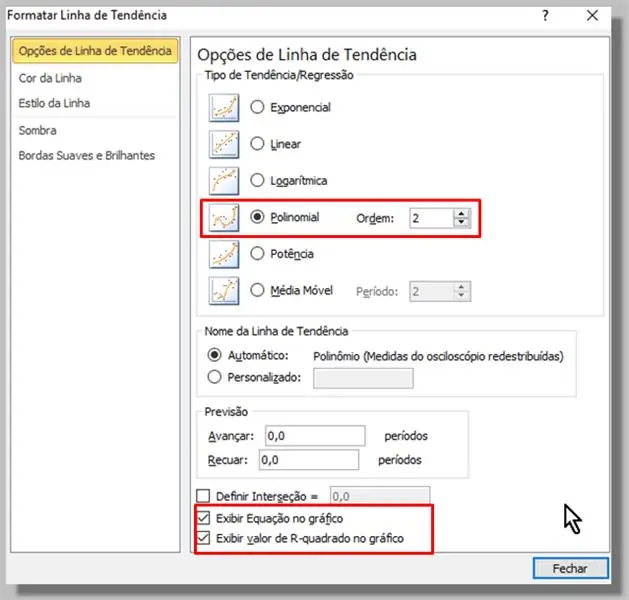
Seleccionando los datos conocidos (puntos azules), al hacer clic y luego hacer clic con el botón derecho, seleccionamos: "Agregar línea de tendencia …"

En la ventana que aparece seleccionamos el tipo Polinomio (el orden 2 será suficiente).

También verificamos las opciones "Ver ecuación en el gráfico" y "Mostrar valor R-cuadrado en el gráfico".

Hacemos clic en "Cerrar".

Paso 13: Rellenar los huecos - Curva polinomial de grado 2

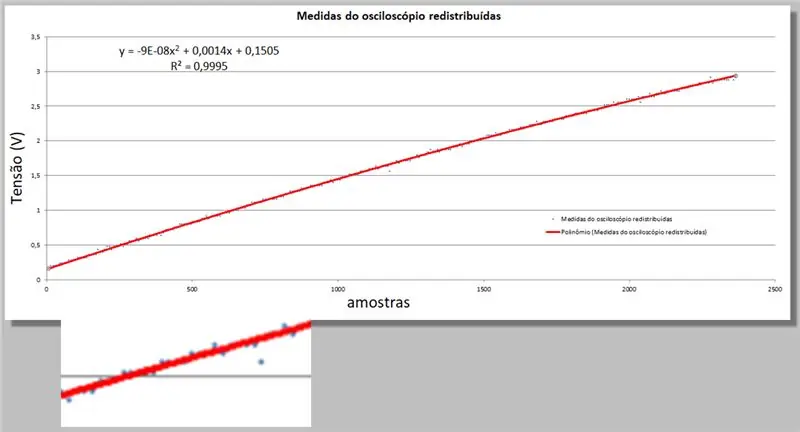
Excel nos brinda dos nuevos datos; la ecuación de segundo orden que mejor se ajusta a los datos y la ecuación R-cuadrado que cuantifica esta adecuación.

Solo recuerda que cuanto más cerca de 1, más apropiada es la ecuación.

No profundicemos en las matemáticas involucradas, usémoslas como una herramienta.

Paso 14: llenar los vacíos: evaluar la función

Completemos las brechas de muestreo con los datos generados por la ecuación. Y luego, compárelos punto por punto.

y = -9E-08x2 + 0, 0014x + 0, 1505

R² = 0, 9999

Voltaje del osciloscopio = -9E-08 * índice2 + 0, 0014 * índice + 0, 1505

Paso 15: Conversión del voltaje del osciloscopio a un valor equivalente para compararlo con el ADC

Aprovechemos esto para transformar también el valor del voltaje del osciloscopio en un valor ADC equivalente.

Como el valor más alto obtenido en el ADP del ESP32 fue 4095, lo que equivale a la lectura de 2.958V para el mismo índice, podemos decir que:

Cada voltio en las medidas del osciloscopio equivale aproximadamente a 1384,4 unidades del AD. Por tanto, podemos multiplicar todas las medidas del osciloscopio por este valor.

Paso 16: Comparación de las dos rampas obtenidas

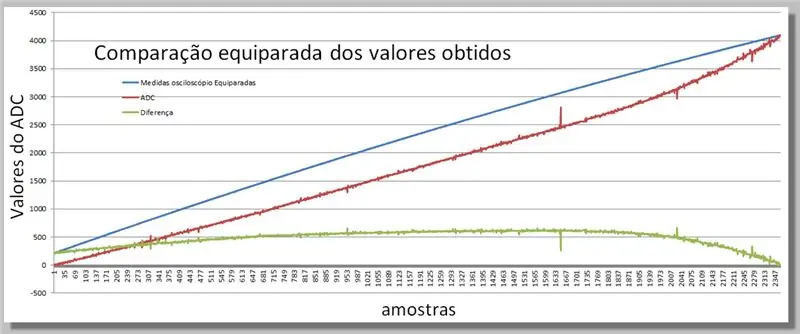
Visualización de las diferencias obtenidas en las dos lecturas.

Paso 17: Comportamiento de la diferencia de lectura de ADC (ERROR)

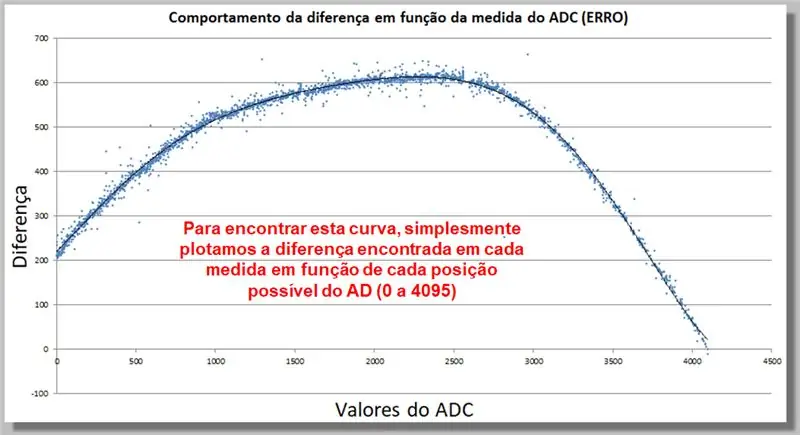
La siguiente curva muestra cómo se comporta la diferencia en la lectura del ADC en función de la medición. Esta recopilación de datos nos permitirá encontrar una función de corrección.

Para encontrar esta curva, simplemente graficamos la diferencia encontrada en cada medida en función de cada posible posición AD (0 a 4095).

Paso 18: Comportamiento de diferencia de lectura de ADC: encontrar una función de corrección

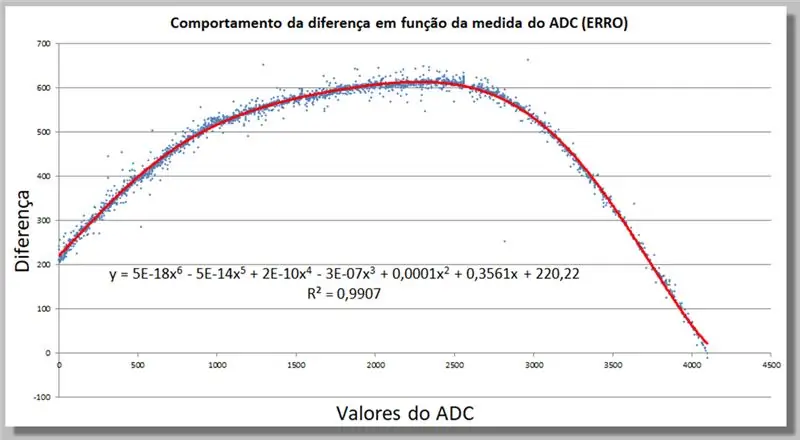
Podemos determinar en Excel una función de corrección agregando una Trend Line, ahora de un grado superior, hasta que encaje suficientemente con nuestros datos.

Paso 19: uso de otro software

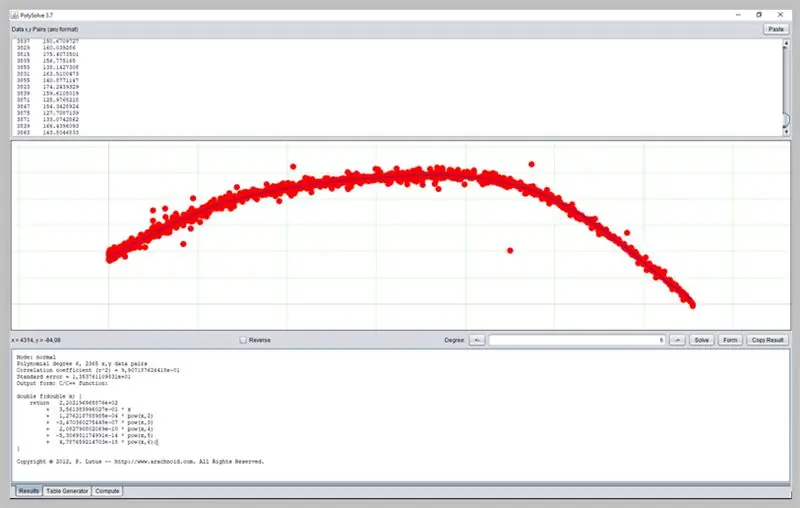
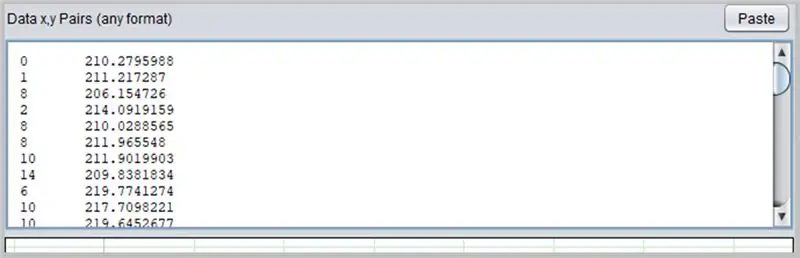
Otro software interesante para determinar curvas es PolySolve, que se puede utilizar directamente en el enlace: https://arachnoid.com/polysolve/ o descargar como aplicación Java.

Permite la aplicación de regresiones polinomiales de mayor grado y la entrega de la función formateada, así como otras funcionalidades.

Para usarlo, simplemente ingrese los datos en el primer cuadro de texto. Los datos deben seguir el orden X, Y separados por una coma o tabulación. Tenga cuidado al usar el punto correctamente como punto decimal.

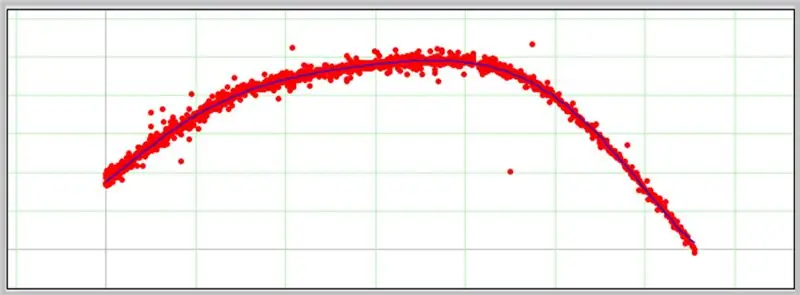
Aparecerá un gráfico en el siguiente cuadro si los datos ingresados tienen el formato correcto.

Así es como fue nuestra curva de error de ADC.

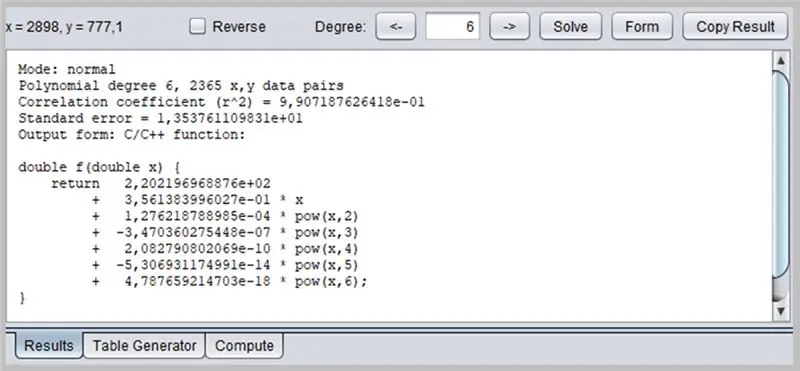
Esta ventana presentará el resultado de la regresión, incluidos los datos de adecuación de la función, que a su vez puede tener su salida formateada de varias formas: como una función C / C ++, una lista de coeficientes, una función escrita en Java, etc.

Nota: preste atención a los separadores decimales

Paso 20: Constantes y configuración ()

Señalo aquí el GPIO utilizado para la captura analógica. Inicializo el puerto serie, así como el pin determinado para la captura analógica.

const int pin_leitura = 36; // GPIO usado para captura analógica void setup () {Serial.begin (1000000); // Iniciciando un porta serial somente para debug pinMode (pin_leitura, INPUT); // Pino utilizado para captura analógica}

Paso 21: Loop () y la función de corrección

Realizamos la captura de la tensión ajustada, e imprimimos los valores con o sin las correcciones correctas.

bucle vacío () {int valor_analogico = analogRead (pin_leitura); // realiza una captura de tensión ajustada //Serial.print(valor_analogico + f (valor_analogico)); // imprime los valores para debug (COM CORREÇÃO) Serial.print (valor_analogico); // imprimime los valores para debug (SEM CORREÇÃO) Serial.print (","); Serial.print (4095); // cria uma linha para marcar o valor máximo de 4095 Serial.print (","); Serial.println (0); // cria uma linha para marcar o valor mínimo de 0}

Observe en la línea 12 que tenemos la opción de imprimir los datos con la adición de la función de diferencia f (valor_análogo).

Paso 22: Uso de la función de corrección PolySolve

Aquí, usamos la función PolySolve dentro del IDE de Arduino.

/ * Modo: normal Polinomio grado 6, 2365 pares de datos x, y Coeficiente de correlación (r ^ 2) = 9, 907187626418e-01 Error estándar = 1, 353761109831e + 01 Forma de salida: Función C / C ++: Copyright © 2012, P. Lutus: https://www.arachnoid.com. Reservados todos los derechos. * / doble f (doble x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e- 10 * potencia (x, 4) + -5,306931174991e-14 * potencia (x, 5) + 4,787659214703e-18 * potencia (x, 6); }

Tenga en cuenta el cambio de coma por punto como separador decimal.

Paso 23: Captura con corrección - Serie del trazador

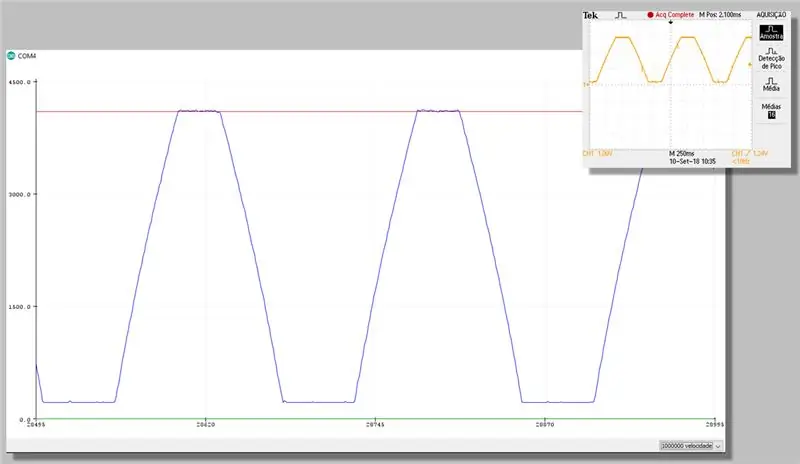
Paso 24: Costo computacional

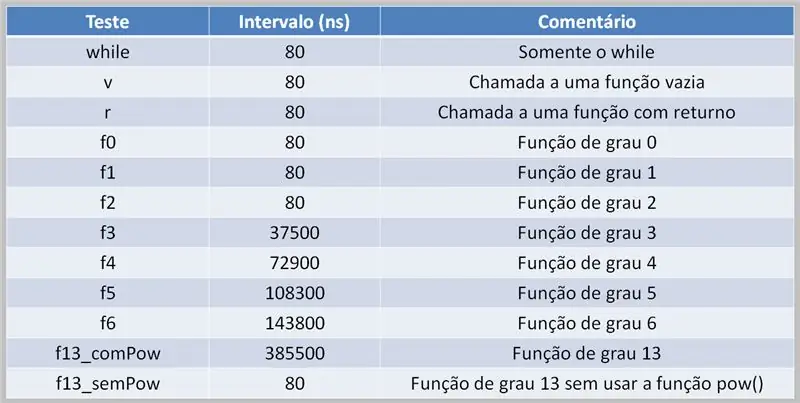
Para realizar cálculos polinomiales, es necesario que el procesador se encargue de esta tarea. Esto puede provocar retrasos en la ejecución, según el código fuente y la potencia informática disponible.

Aquí, vemos una tabla de resultados de una prueba que usa polinomios de varios grados. Observe la diferencia entre las veces que se usó la función pow () y cuando no.

Paso 25: Código de prueba: configuración () e inicio de bucle ()

Aquí, tenemos el código utilizado en nuestra prueba.

configuración vacía () {Serial.begin (1000000); // Iniciando un porta serial somente para debug} void loop () {float valor_analogico = 500.0; // um valor arbtrario float quantidade = 10000.0; // cuantidade de chamadas float contador = 0.0; // contador de chamadas

Paso 26: Código de prueba: bucle () y procesamiento

Usé la función micros () para obtener el valor en microsegundos.

// ============= inicia o proceso float agora = micros (); // marca o instante inicial while (contador <quantidade) {// v (valor_analogico); // função vazia // r (valor_analogico); // função com retorno // f0 (valor_analogico); // grau 0 // f1 (valor_analogico); // grau 1 // f2 (valor_analogico); // grau 2 // f3 (valor_analogico); // grau 3 // f4 (valor_analogico); // grau 4 // f5 (valor_analogico); // grau 5 // f6 (valor_analogico); // grau 6 // f13_semPow (valor_analogico); // grau 13º SEM a função POW // f13_comPow (valor_analogico); // grau 13º COM a função POW contador ++; } agora = (micros () - agora) / quantidade; // determina o intervalo que se passou para cada iteração // ============= finaliza o processo

Paso 27: Código de prueba - Bucle () - Resultados

Imprimimos el valor devuelto por la función de grado 13 con y sin POW para comparar, así como el intervalo de procesamiento.

// imprime o valor retornado da função de grau 13 com e sem POW para comparação Serial.print (f13_semPow (valor_analogico)); // grau 13º SEM a função POW Serial.print ("-"); Serial.print (f13_comPow (valor_analogico)); // grau 13º COM a função POW Serial.print ("-"); // imprime el intervalo del proceso Serial.println (agora, 6); }

Paso 28: Código de prueba - Funciones utilizadas

Funciones vacías (solo con retorno) de grado 0 y 1.

// FUNÇÃO VAZIAdouble v (doble x) {} // FUNÇÃO SOMENTE COM RETORNO double r (doble x) {return x; } // FUNÇÃO DE GRAU 0 doble f0 (doble x) {return 2.202196968876e + 02; } // FUNÇÃO DE GRAU 1 doble f1 (doble x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x; }

Funciones de grado 2, 3 y 4.

// FUNÇÃO DE GRAU 2double f2 (doble x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2); } // FUNÇÃO DE GRAU 3 doble f3 (doble x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3); } // FUNÇÃO DE GRAU 4 doble f4 (doble x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4); }

Funciones de grado 5 y 6.

// FUNÇÃO DE GRAU 5double f5 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5); } // FUNÇÃO DE GRAU 6 doble f6 (doble x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }

Función de grado 13 usando el POW.

// FUNÇÃO DE GRAU 13 USANDO O POWdouble f13_comPow (doble x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow (x, 2) + -3, 968558178426e-06 * pow (x, 3) + 1, 047910519933e-08 * pow (x, 4) + -1, 479271312313e-11 * pow (x, 5) + 1, 220894795714e-14 * pow (x, 6) + -6, 136200785076e-18 * pow (x, 7) + 1, 910015248179e-21 * pow (x, 8) + -3, 566607830903e-25 * pow (x, 9) + 5, 000280815521e-30 * pow (x, 10) + 3, 434515045670e-32 * pow (x, 11) + -1, 407635444704e-35 * pow (x, 12) + 9, 871816383223e-40 * pow (x, 13); }

Función de grado 13 sin usar POW.

// FUNÇÃO DE GRAU SEM USAR O POWdouble f13_semPow (doble x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * x * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + 1, 220894795714e-14 * x * x * x * x * x * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x * x + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + -1, 407635444704e-35 * x * x * x * x * x * x * x * x * x * x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x * x; }

Paso 29: Archivos

Descarga los archivos:

PDF

INO

Hoja de cálculo