Observando la receta de su globo ocular: un proyecto BME60B: 9 pasos

2025 Autor: John Day | [email protected]. Última modificación: 2025-01-23 14:39

Por: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste

El aumento es una de las características clave presentes en las gafas de lectura, que se clasifican por su graduación de dioptrías. Según la Universidad de Tecnología de Michigan, una dioptría es una distancia focal de la lente, generalmente medida en mm, en la unidad de metros (Universidad de Tecnología de Michigan). Debido a que los anteojos para leer tienen lentes convexos, la distancia focal sería positiva, lo que haría que las dioptrías también fueran positivas (HyperPhysics). La distancia focal aumenta a medida que la distancia entre el objeto se aleja de la lente real, y esto hace que las dioptrías disminuyan ya que son inversamente proporcionales. Por lo tanto, tener anteojos de lectura con dioptrías adicionales ayudaría a la lente a ampliar la vista de modo que pueda parecer que la distancia focal es menor al aumentar el valor de las dioptrías.

El código presentado se utilizará para predecir la dioptría de una lente con una prescripción desconocida. Se utilizan dos entradas para calcular la prescripción: una fotografía del fondo controlado sin usar lentes, y otra fotografía del mismo fondo pero a través del lente elegido. El programa medirá la distorsión entre estas dos fotografías. A partir de ahí, podremos estimar las dioptrías de la lente y producir un resultado para que el usuario lo vea.

Para este Instructable, necesitará:

• Un patrón de tablero de ajedrez en blanco y negro impreso en una hoja de papel de 11 x 8,5 pulgadas
• Una cámara con la capacidad de bloquear su enfoque.
• Un trípode o algo similar para asegurar la cámara.
• Varias recetas de gafas para leer.
• MATLAB

Paso 1: toma fotos

Para calcular la ampliación de una lente, debe poder compararla con el tamaño real del objeto. Para este proyecto, compararemos una imagen ampliada con una imagen de control.

Por lo tanto, el primer paso es tomar dos fotos de la misma imagen: la primera solo a través de la cámara y la segunda a través del lente de las gafas de lectura que desea probar.

Tomarás una fotografía de un tablero de ajedrez en blanco y negro de 8.5x11 pulgadas con una cuadrícula de 1 pulgada. Configure su cámara a 11 pulgadas de distancia del tablero de ajedrez. Antes de tomar las fotos, bloquee el enfoque en el tablero de ajedrez.

Tome una foto del tablero de ajedrez sin las gafas para leer. Luego, sin mover nada, coloque las gafas de lectura frente a la cámara y tome la segunda foto.

Asegúrese de que la posición de su cámara no se mueva entre tomas. Lo único que debería cambiar entre las dos fotos es la presencia de la lente de las gafas frente a la cámara.

Cuando haya terminado con las fotos, cárguelas en su computadora.

Paso 2: cargue las imágenes en MATLAB

Abra una nueva secuencia de comandos.

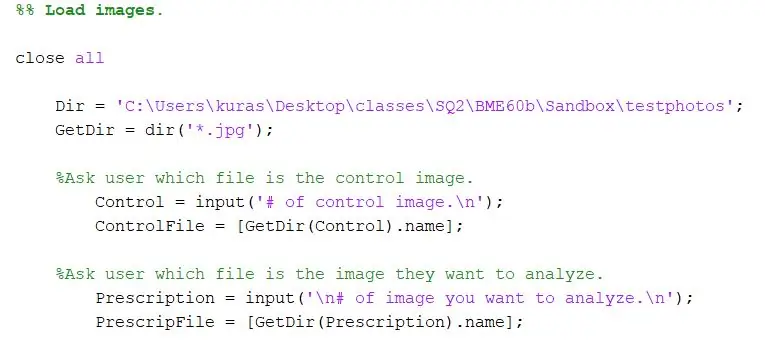
Primero, especifique el directorio donde se almacenan las fotos. Luego, use la función dir para extraer imágenes-j.webp

Dir = 'C: / Users / kuras / Desktop / classes / SQ2 / BME60b / Sandbox / testphotos'; GetDir = dir ('*. Jpg');

Para nuestro proyecto, queríamos preguntarle al usuario del programa qué archivos querían comparar. La primera sección le pide al usuario que especifique la imagen de control y la segunda le pide al usuario que especifique la imagen de prueba.

• % Pregunte al usuario qué archivo es la imagen de control.
• Control = input ('# de imagen de control. / N');
• ControlFile = [GetDir (Control).name]
• % Pregunte al usuario qué archivo es la imagen que desea analizar.
• ChooseFile = input ('\ n # de imagen que desea analizar. / N');
• PrescripFile = [GetDir (ChooseFile).name];

Paso 3: análisis de imágenes

Una imagen coloreada en MATLAB es de tamaño MxNx3, mientras que una imagen en escala de grises es MxN. Esto significa que es más rápido mejorar / editar una imagen en escala de grises porque hay menos datos de los que realizar un seguimiento. Utilice rgb2gray para convertir la imagen a escala de grises. (Se usó la función de imrotación porque nuestras fotos venían en horizontal; esta línea de código puede ser necesaria o no en su versión).

• % convertir a escala de grises y rotar
• I = imread (ControlFile);
• I = rgb2gray (I);
• I = rotar (I, 90);

A continuación, muestre la imagen. La función de subtrama se utiliza para que la imagen de prueba pueda estar junto al control en pasos posteriores.

• %monitor
• Figura 1);
• subtrama (1, 2, 1)
• imshow (yo);
• título (ControlFile);

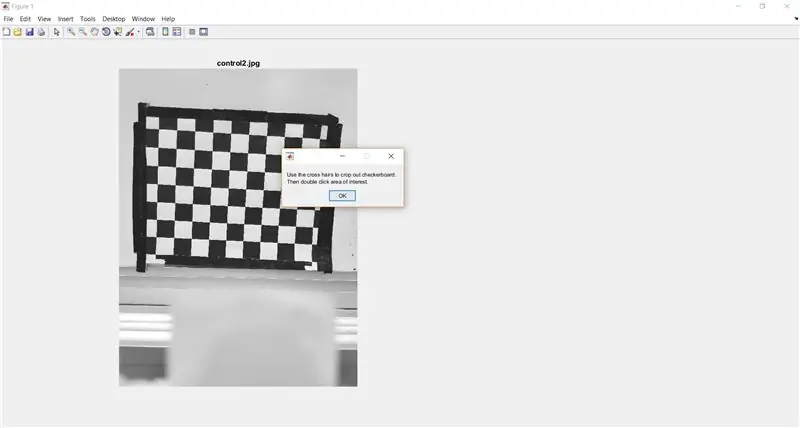
Utilice imcrop para pedirle al usuario que recorte el tablero de ajedrez de la imagen completa. El siguiente código también muestra un cuadro de mensaje para proporcionar instrucciones al usuario.

• % recortar tablero de ajedrez para su análisis
• waitfor (msgbox ({'Use la cruz para recortar el tablero de ajedrez.', 'Luego haga doble clic en el área de interés.'}));
• I_crop = imcrop (I);

Utilice imbinarize para binarizar la imagen.

I_binary = imbinarize (I_crop);

Paso 4: Calcule el ancho de los cuadrados blancos en el tablero de ajedrez

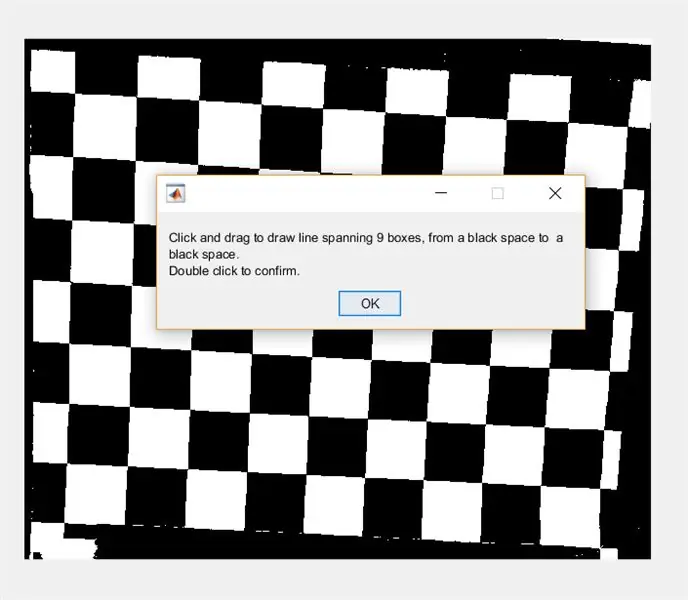
A continuación, solicite al usuario que dibuje una línea a través de la imagen usando imline. Esta línea debe correr horizontalmente a través del tablero de ajedrez. Debe comenzar y terminar en un cuadrado negro (no importa dónde); esto se debe a que mediremos el ancho de los cuadrados blancos, no los negros.

• %Dibujar linea
• Figura 1)
• subtrama (1, 2, 1)
• imshow (I_binary);
• waitfor (msgbox ({'Haga clic y arrastre para dibujar una línea que abarque 9 cuadros, desde un espacio negro a un espacio negro.', 'Haga doble clic para confirmar.'}));
• línea = imline;
• posición = esperar (línea);
• puntos finales = line.getPosition;

Extraiga las coordenadas X e Y de los puntos finales de la línea dibujada.

• X = puntos finales (:, 1)
• Y = puntos finales (:, 2);

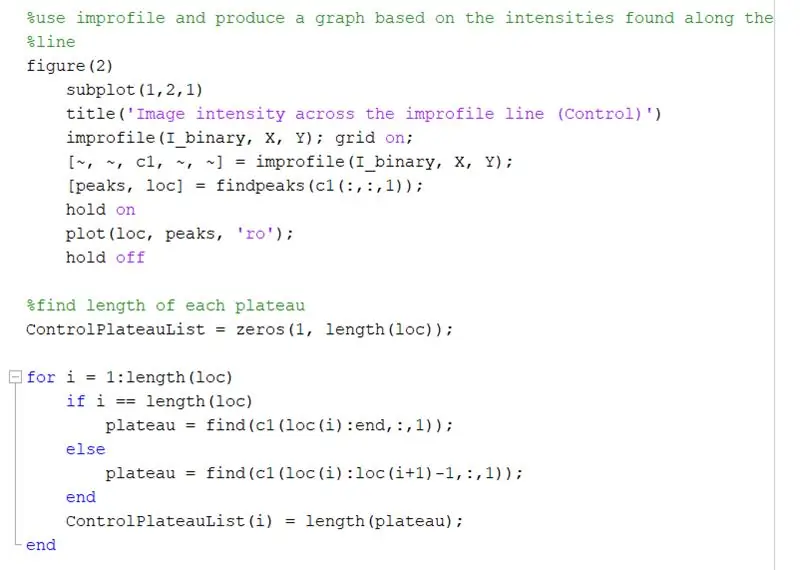
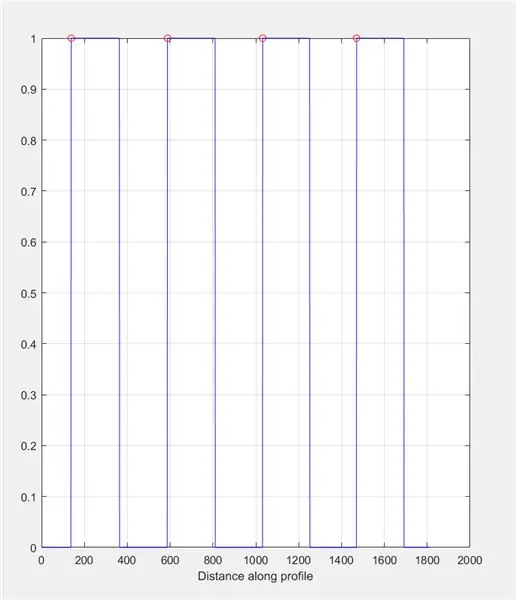
Utilice improfile para producir un gráfico basado en las intensidades encontradas a lo largo de la línea dibujada. Esto debería parecerse a una onda cuadrada que va de 0 (negro) a 1 (blanco). Calcula también los picos y sus ubicaciones.

• Figura 2)
• subtrama (1, 2, 1)
• title ('Intensidad de la imagen en la línea de improfile (Control)')
• improfile (I_binary, X, Y); cuadrícula activa;
• [~, ~, c1, ~, ~] = improfile (I_binary, X, Y);
• [picos, loc] = encontrar picos (c1 (:,:, 1));
• esperar
• plot (loc, picos, 'ro');
• esperar

Encuentre la longitud de cada meseta en el gráfico de improfile usando un bucle for. Ejecute el ciclo for para la misma cantidad de picos que hay en el gráfico de improfile. Para calcular la longitud de cada meseta, utilice la función "buscar" para encontrar todas las ubicaciones donde hay un valor de intensidad "1" en lugar de "0". Luego, calcule la longitud de esa matriz para obtener la longitud total de la meseta, que debería ser igual al ancho de un cuadrado blanco en píxeles. ControlPlateauList = zeros (1, length (loc));

para i = 1: longitud (loc)

si i == longitud (loc)

meseta = encontrar (c1 (loc (i): fin,:, 1));

demás

meseta = encontrar (c1 (loc (i): loc (i + 1) -1,:, 1));

fin

ControlPlateauList (i) = longitud (meseta);

fin

Paso 5: repita los pasos 3 y 4 para la imagen de prueba

* Nota: al dibujar la línea de improfile en la imagen de prueba, asegúrese de dibujarla a través de los cuadrados que corresponden a la línea que dibujó en la imagen de control.

Paso 6: Calcule la ampliación de la lente

Las medidas ampliadas se calculan dividiendo la media de la longitud de la meseta, que se calculó en el paso 5, por la media de la longitud de la meseta de control, que se calculó en el paso 4. Se calcula que es 1,0884.

aumento = media (plateauList) / media (ControlPlateauList);

Paso 7: encontrar R-cuadrado y la prescripción del usuario mediante interpolación

Usando el código:

• md1 = fitlm (GivenPrescription, MagArray);
• Rsquared = md1. Rsquared. Ordinary;

Podemos encontrar el valor R-cuadrado del gráfico GivenPresciption (valores dados de nuestras lentes) frente a MagArray (una matriz de las proporciones de medidas de aumento que calculamos anteriormente). Al tener un valor de R cuadrado lo suficientemente alto, se puede inferir que existe una correlación lo suficientemente fuerte como para justificar el uso de este método. Para este caso particular, el valor de R cuadrado fue 0,9912, lo que sugiere una fuerte correlación y, por lo tanto, se justifica el uso de este método en el análisis.

Usando la función:

Prescription = interp1 (MagArray, GivenPrescription, magnificación, 'lineal');

Podemos interpolar el valor de prescripción correspondiente (en el eje x) de nuestra relación de aumento (un valor en el eje y) y encontrar cuál es la prescripción del usuario.

La interpolación de datos es importante para que este método funcione, ya que nos permite hacer suposiciones sobre la información que no tenemos, en función de la información que tenemos. Si bien una línea de mejor ajuste técnicamente sería un candidato más fuerte para esta suposición, la creación de límites para reducir la cantidad de salidas tiene el mismo efecto que los anteojos recetados con valores uniformes incrementales de todos modos. Esto se explica en pasos posteriores.

Paso 8: Mostrar la prescripción del usuario en un gráfico

Usando el siguiente código:

• figura;
• trama (GivenPrescription, MagArray, '-g')
• esperar
• trama (prescripción, aumento, 'pb')
• esperar
• red
• leyenda ('Datos', 'Puntos interpolados', 'Ubicación', 'NW')

Podemos trazar un gráfico que muestre las relaciones de aumento frente a la prescripción dada con una línea verde y los datos encontrados de nuestro aumento calculado frente a nuestra prescripción interpolada con una estrella azul. Luego, la leyenda etiqueta el título, el eje xy el eje y, y coloca la leyenda en la esquina superior izquierda.

Paso 9: Reduzca su prescripción

El siguiente código se utiliza para generar el redondeo de la prescripción:

• si Receta <= 1.125

  CalculatedPrescription = '1.0';

• elseif Receta <= 1.375

  CalculatedPrescription = '1,25';

• elseif Receta <= 1.625

  CalculatedPrescription = '1.5';

• elseif Receta <= 1.875

  CalculatedPrescription = '1,75';

• elseif Receta <= 2.25

  CalculatedPrescription = '2.0';

• elseif Receta <= 2.625

  CalculatedPrescription = '2.5';

• elseif Receta <= 3

  CalculatedPrescription = '2.75';

• elseif Receta <= 3.375

  CalculatedPrescription = '3.25';

• demás

  CalculatedPrescription = 'desconocido';

• fin

La prescripción encontrada a través de la interpolación no refleja necesariamente la prescripción real; esto se debe a que siempre habrá ligeras variaciones en el análisis de la foto debido a un error humano. Por lo tanto, necesitamos este paso para clasificar la prescripción real.

Las prescripciones que se dan suelen empezar a partir de 1,0 dioptrías y aumentan en 0,25 en sus prescripciones, por lo que tras calcular la prescripción queremos determinar la prescripción que mejor se adapta a lo que pueda necesitar el usuario. Después de calcular la prescripción, la ejecutamos a través de las declaraciones If proporcionadas para verificar su valor y determinar qué prescripción es necesaria. Cualquier cantidad menor o igual a 1.125, entonces la prescripción es 1.0. Cualquier cantidad menor o igual a 1.375, la prescripción es 1.25. Cualquier cantidad menor o igual a 1.625, la prescripción es 1.5. Cualquier cantidad menor o igual a 1.845, la prescripción es 1.75. Etcétera.

Tenemos los valores aumentando ya que estamos comprobando si los valores son menores que. Si hiciéramos que los valores fueran decrecientes, entonces la primera instrucción if leería la primera instrucción if todo el tiempo. Si la prescripción es la más pequeña, queremos que la reconozca como la más pequeña de inmediato, por eso el valor más pequeño es el que comenzamos. Cualquier valor superior al valor más alto significa que la prescripción no está dentro del rango de nuestros datos, por lo que dará la lectura de cadena "Desconocida".